A geometry problem by Yahia El Haw

Geometry Level 2

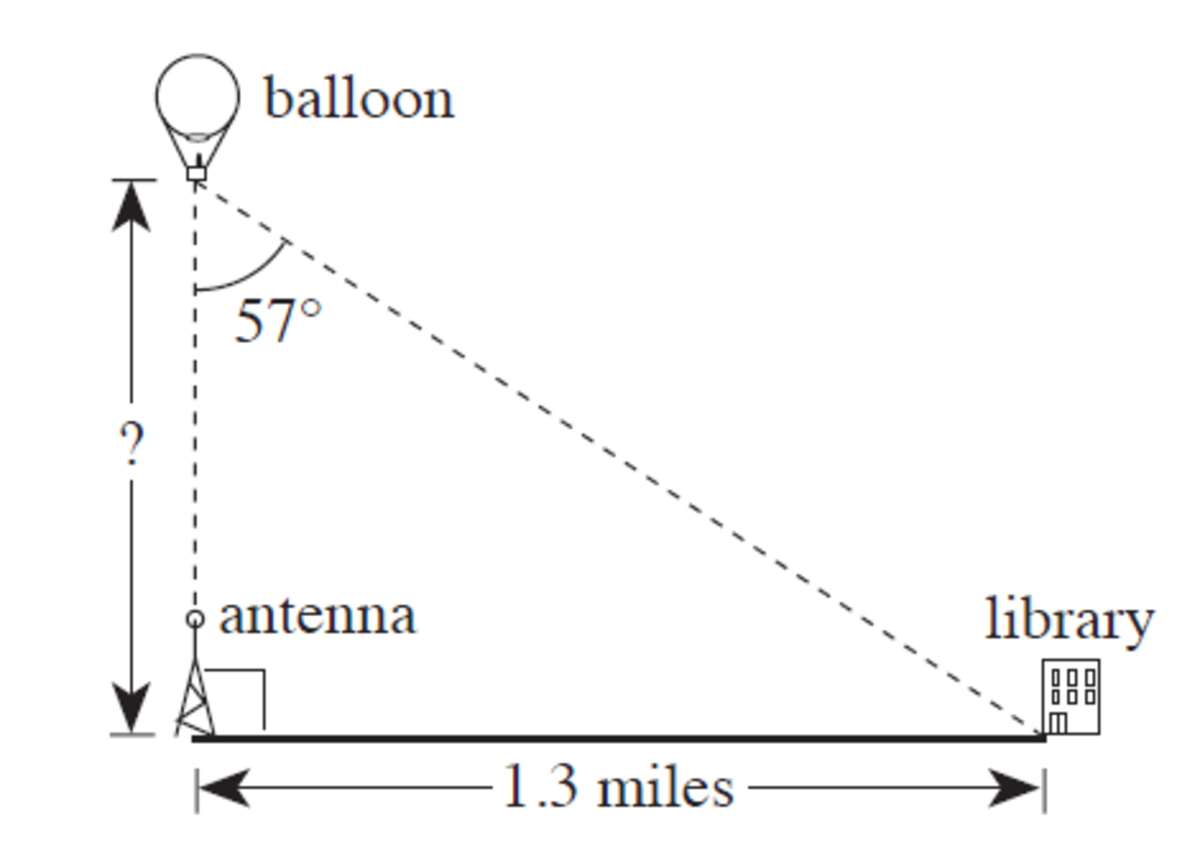
From a hot air balloon, the angle between a radio antenna straight below and the base of the library downtown is 57°, as shown below. If the distance between the radio antenna and the library is 1.3 miles, how many miles high is the balloon?

1.3 sin ⁡ 57 ∘ \large\frac { 1.3 }{ \sin { { 57 }^{ \circ } } } 1.3 tan ⁡ 57 ∘ \large1.3\tan { { 57 }^{ \circ } } 1.3 sin ⁡ 57 ∘ \large1.3\sin { { 57 }^{ \circ } } 1.3 tan ⁡ 57 ∘ \large\frac { 1.3 }{ \tan { { 57 }^{ \circ } } } 1.3 cos ⁡ 57 ∘ \large\frac { 1.3 }{ \cos { { 57 }^{ \circ } } }

Yahia El Haw by Yahia El Haw , 18, Egypt

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Let x x be the height of the balloon, then we have

tan ⁡ 57 = opposite side adjacent side = 1.3 x \tan 57=\dfrac{\text{opposite side}}{\text{adjacent side}}=\dfrac{1.3}{x} or x = 1.3 tan ⁡ 57 x=\boxed{\dfrac{1.3}{\tan 57}} .

1 Helpful 1 Interesting 1 Brilliant 0 Confused

S O H − C A H − T O A SOH-CAH-TOA

S O H : sin ⁡ θ = o p p o s i t e h y p o t e n u s e SOH:\sin\theta=\dfrac{opposite}{hypotenuse}

C A H : cos ⁡ θ = a d j a c e n t h y p o t e n u s e CAH:\cos\theta=\dfrac{adjacent}{hypotenuse}

T O A : = tan ⁡ θ = o p p o s i t e a d j a c e n t TOA:=\tan\theta=\dfrac{opposite}{adjacent}

tan ⁡ 57 = 1.3 h \tan57=\dfrac{1.3}{h}

h = 1.3 tan ⁡ 57 h=\dfrac{1.3}{\tan57}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...