A Sangaku geometry problem

It's clear that $\overline{A E} = \frac{R_1}{2}$ because $\angle ACE = 30^{o}$ .

The triangle $\Delta AHF$ has sides $\overline{AH} = \frac{R_1}{2} + R_2$ , $\overline{HF} = R_2$ and $\overline{AF} = R_1$ . Furthermore angle $\angle AHF = 120^{o}$ . Using cosine law:

$\large \displaystyle R_1^2 = \left (\frac{R_1}{2} + R_2 \right)^2 + R_2^2 - 2 \left (\frac{R_1}{2} + R_2 \right) R_2 \cos(120^{o})$

$\large \displaystyle R_1^2 = \frac{R_1^2 + 4R_1R_2 + 4R_2^2}{4} + R_2^2 + \frac{2R_2R_1 + 4R_2^2}{4}$

$\large \displaystyle 12R_2^2 + 6R_1R_2 - 3R_1^2 = 0$

$\large \displaystyle 4R_2^2 + 2R_1R_2 - R_1^2 = 0$

$\large \displaystyle R_2 = \frac{-2R_1 + \sqrt{20R_1^2}}{8}$

$\color{#20A900} \boxed{\large \displaystyle R_2 = R_1 \left( \frac{-1 + \sqrt{5}}{4} \right)}$

Thus:

$\color{#3D99F6} \boxed{\large \displaystyle \frac{R_2}{R_1} \approx 0.309017 }$

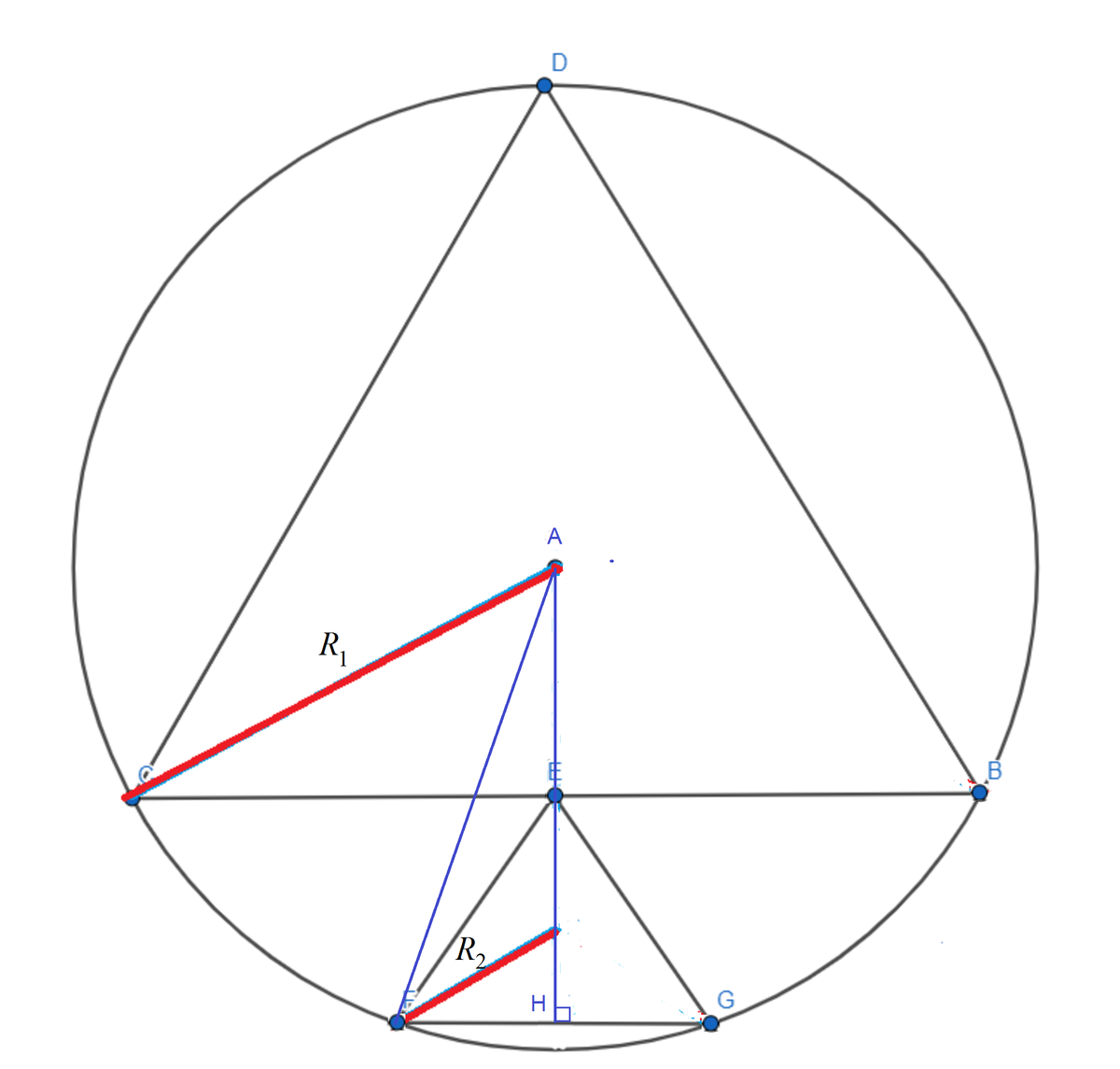
Let $R_1 = 1$ and $R_2 = r$ . Then $\dfrac {R_2}{R_1} = r$ . Let the centroid of $\triangle BCD$ be $A$ and the median of $\triangle EFG$ be $EH$ . Then we note that $AE$ and $EH$ are colinear and is perpendicular to $FG$ . By Pythagorean theorem , we have:

$\begin{aligned} AH^2 + FH^2 & = AF^2 \\ (AE+EH)^2 +FH^2 & = AF^2 \\ \left(\frac 12 + \frac 32 r \right)^2 + \left(\frac {\sqrt 3}2r\right)^2 & = 1 \\ 9r^2 + 6r + 1 + 3r^2 & = 4 \\ 12r^2 + 6r - 3 & = 0 \\ 4r^2 + 2r - 1 & = 0 \end{aligned}$

$\implies r = \dfrac {\sqrt{2^2-4(-1)(4)}-2}8 = \dfrac {\sqrt 5 -1}4 \approx \boxed{0.309}$