A geometry test #3

Since ABC is an isosceles right triangle where AB=AC; we can deduce that:

• AM is the median line to BC, the angle bisector of $\widehat{BAC}$ and the perpendicular line to BC.

• $\widehat{ABC}=\widehat{ACB}=45^{o}$

• The median line AM is half the hypotenuse BC. Therefore, $AM=BM=CM$ .

Therefore, $\widehat{BAM}=\widehat{CAM}=\frac{\widehat{ABC}}{2}=\frac{90^{o}}{2}=45^{o}$ .

We can clearly see that $\widehat{MAD}+\widehat{ADM}=90^{o}$ (Since AMD is a right triangle) and $\widehat{HBD}+\widehat{HDB}=90^{o}$ (Since HBD is a right triangle).

Therefore, $\widehat{MAD}+\widehat{ADM}=\widehat{HBD}+\widehat{HDB}$ . As $\widehat{ADM}$ and $\widehat{HDB}$ are vertically opposite angles, $\widehat{HDB}=\widehat{ADM}$ .

Hence, $\widehat{MAD}=\widehat{HBD}$ .

We see that $\widehat{CAK}=\widehat{CAM}+\widehat{DAM}=45^{o}+\widehat{DAM}$ and $\widehat{ABH}=\widehat{ABC}+\widehat{DBH}=45^{o}+\widehat{DBH}$ .

Since $\widehat{MAD}=\widehat{HBD}$ , $\widehat{CAK}=\widehat{ABH}$ .

Hence we can deduce that 2 right triangles AKC and BHK are congruent (Hypotenuse-Acute Angle).

Therefore, $AK=BH$ .

We can also deduce that 2 triangles AKM and BHM are congruent (Side-Angle-Side). Therefore $\widehat{AMK}=\widehat{HMD}$ .

We can see that: $\widehat{AMK}$ and $\widehat{KMD}$ are complementary angles. Since $\widehat{AMK}=\widehat{HMD}$ , $\widehat{KMD}$ and $\widehat{KMD}$ are complementary angles, which also means that $\widehat{HMK} = \boxed{90^{o}}$

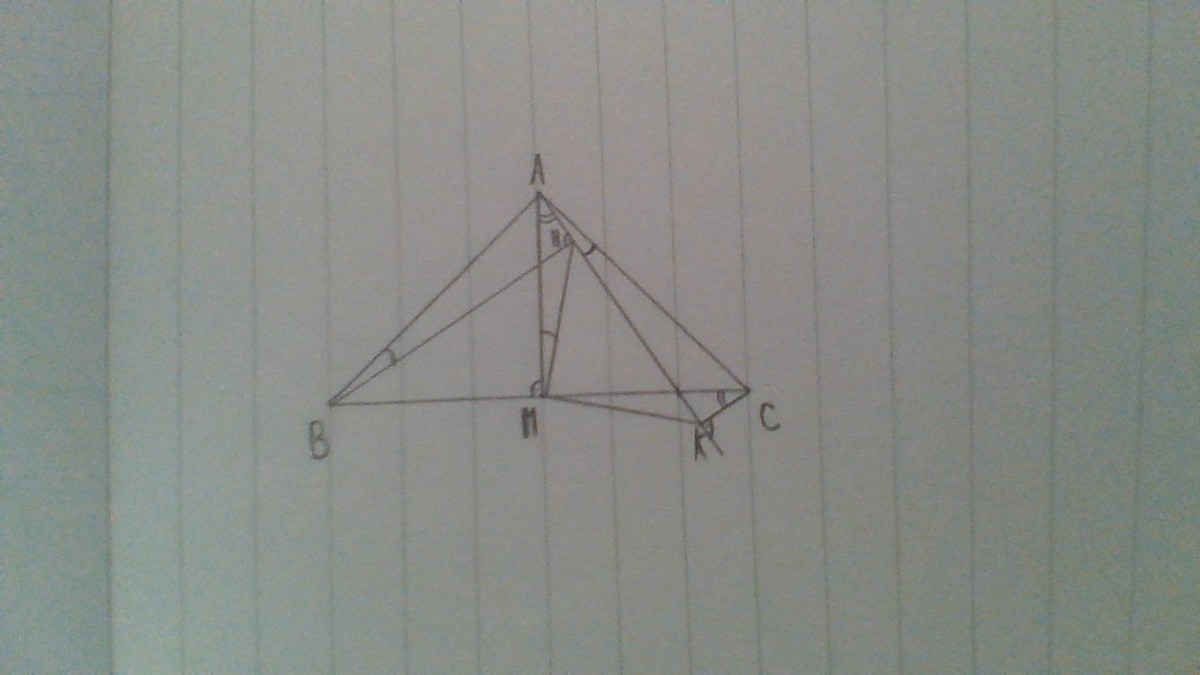According to Thales's theorem quadrilateral AHMB is cyclic. And because it is cyclic we can use Inscribed angle theorem to show that angles ABH and AMH are congruent. And by calculating the value of the angle KAC we can easly conclude that it is equal to the value of the angle ABH. And because the triangle ABC is isosceles we know that |AB|=|AC| so triangles ABH and AKC are congruent (same angles and same hypotenuse), by this we can know that |AH|=|CK|. And again because the triangle ABC is right and isosceles we know that |AM|=|MC|. Now because triangles ABH and AKC are congruent we know that angles ACK and BAH are congruent, we can calculate from this that angles MAK and MCK are also congruent. And by this information we can conclude that triangles AHM and CKM are congruent so the angles AMH and CMK are also congruent. That means that the angle HMK is only rotated angle AMC, so |HMK|=90°.

Place $\triangle ABC$ on a coordinate plane so that $A$ is at the origin, $B$ is on the $y$ -axis at $(b, 0)$ , and $C$ is on the $x$ -axis at $(0, b)$ .

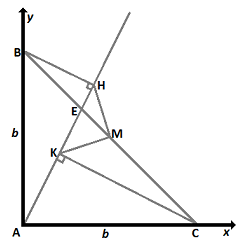
The midpoint of $BC$ is $M(\frac{b}{2}, \frac{b}{2})$ .

Let $AE$ have the equation $y = mx$ . Since $BH$ is perpendicular to $y = mx$ and through $(b, 0)$ it has the equation $y = -\frac{1}{m}x + b$ and intersects $y = mx$ at $H(\frac{bm}{m^2 + 1}, \frac{bm^2}{m^2 + 1})$ , and since $CK$ is perpendicular to $y = mx$ and through $(0, b)$ it has the equation $y = -\frac{1}{m}x + \frac{b}{m}$ and intersects $y = mx$ at $K(\frac{b}{m^2 + 1}, \frac{bm}{m^2 + 1})$ .

The slope of $HM$ is $m_{HM} = \frac{\frac{b}{2} - \frac{bm^2}{m^2 + 1}}{\frac{b}{2} - \frac{bm}{m^2 + 1}} = -\frac{(m + 1)}{(m - 1)}$ , and the slope of $KM$ is $m_{KM} = \frac{\frac{b}{2} - \frac{bm}{m^2 + 1}}{\frac{b}{2} - \frac{b}{m^2 + 1}} = \frac{(m - 1)}{(m + 1)}$ . Since $m_{HM}m_{KM} = -\frac{(m + 1)}{(m - 1)} \cdot \frac{(m - 1)}{(m + 1)} = -1$ , $HM$ and $KM$ are perpendicular, so $\angle HMK = \boxed{90°}$ .