A giant disc and tiny balls

Classical Mechanics Level 5

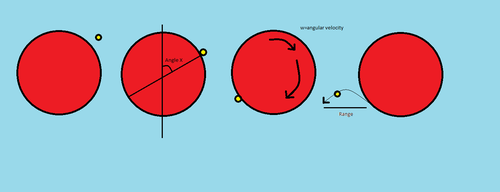Suppose a very massive disc is there, which was initially at Rest with its centre pivoted in to a vertical wall, And i drop balls upon it from rest/negligible initial velocity the balls stick to the disc at angle 'x' with the vertical, the disc rotates along with them and the balls leave the disc tangentially flying off at the point diametrically opposite And several several such balls are dropped in similar fashion continuously without breaks, "All collisions are inelastic", and "balls are very light compared to disc" . Then it turns out that the disc after some time reaches a saturation angular velocity, that is the process becomes smooth and angular acceleration of disc ceases,

Then find the value of 'sin(x)' (the angle) for which the balls leaving tangentially will reach maximum range on ground when the disc has attained the constant angular velocity

Refer to figure for getting a clearer picture, only one ball has been shown for clarity

NOTE

1) The problem is simpler than it looks

2) Calculus not required, but if you do it using calculus, do share your method

3) Carefully observe and ask yourself, why does the disc rotate, who provides the energy, and where does the system ever lose energy to attain saturation, and if so what should be the criteria satisfied for reaching that state


The answer is 0.577.

View wiki
Mvs Saketh by Mvs Saketh , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Mvs Saketh
Dec 24, 2014

Let us carefully observe, the system gains energy from gravity and loses in the inelastic collisions that happen between the initially stationary balls and the rotating cylinder.

Then it is only logical that the disc will revolve with same angular velocity when the drop in its angular velocity due to successive collisions is equal to the gain in angular velocity due to the fall in potential energy when the balls move to the diametrically opposite end

Now you might say, that there is a time lag between the two processes , then how and what makes me say that the system attains uniform velocity, well note that it is not one ball or some discrete balls but infinite small balls continuosly flowing, so it is not that some balls are falling and rotating with the system and leaving but more that when some balls have joined the rotating disc, some other balls have already imparted their contribution and are about to jump off,

Now lets bring in the math,

Consider first the loss in angular velocity due to collisions

Consider the contribution of a single ball

since initially the ball was at rest, there is no angular impulse imparted, hence

I w = ( I + d I ) ( w − d w ) d w = d I I w Iw=(I+dI)(w-dw)\\ \\ dw=\frac { dI }{ I } w

dI is the small rise in moment of inertia when a ball joins the disc, , Now consider the time when the ball reaches the diametric opposite end, what is the gain in w then,

2 ( d m ) g R c o s ( x ) = ( I + d I ) 2 ( w + d w ) 2 − ( I + d I ) 2 w 2 ≃ ( I + d I ) 2 ( 2 w d w ) ≃ I w d w 2(dm)gRcos(x)=\frac { (I+dI) }{ 2 } (w+dw)^{ 2 }-\frac { (I+dI) }{ 2 } { w }^{ 2 }\simeq \quad \frac { (I+dI) }{ 2 } (2wdw)\quad \simeq \quad Iwdw

(dm is the mass of ball )

2 ( d m ) g R c o s ( x ) I w = d w \frac { 2(dm)gRcos(x) }{ Iw } =dw

Note that in this process, moment of inertia remains unchanged,

Now there is no change in w when the ball leaves the disc because it leaves with no relative velocity (just like a cars velocity wont change if you simply slip off from the side, unless you jump off it with a relaitive velocity,)(or sand sliding off a cart)

Equating the loss and gain we have

2 ( d m ) g R c o s ( x ) I w = w d I I \frac { 2(dm)gRcos(x) }{ Iw } =\frac { wdI }{ I }

Now cancelling like terms and isolating w and using dI=dm (r)^2

w = 2 g c o s ( x ) R \\ w=\sqrt { \frac { 2gcos(x) }{ R } }

Now all the balls leave at this angular velocity tangentially making angle x with horizontal,

and range is given by

w 2 R 2 s i n ( 2 x ) g = 2 R c o s ( x ) s i n ( 2 x ) \frac { { w }^{ 2 }{ R }^{ 2 }sin(2x) }{ g } =2Rcos(x)sin(2x)

which is max at

s i n ( x ) = 1 3 sin(x)=\frac { 1 }{ \sqrt { 3 } } \\

which is nothing but 0.577

5 Helpful 0 Interesting 0 Brilliant 1 Confused

You might think that once flow has been established, since the number of balls on the disc at a given time is fixed, how the hell is moment of inertia changeing when new balls come in which is to say that one might wrongly reason that since equal number of balls enter and exit at given time interval, so moment of inertia of system (balls + disc ) doesnt change on addition of new balls,, But look more closely and convince yourself, what if there was no gravity, , then will the balls fly off? Yes because it is a condition given in question except they would fly off straightly tangentially off instead of dropping on ground or ever coming to rest, so whilst they have left the disc long ago, still they have the angular momentum that they took during their brief time on the disc, and even these distant balls are part of our system,, and hence the contribution of new balls starting from rest does indeed cause a change in moment of inertia, pardon me if i am unable to explain properly, but this is something you must yourself understand

Mvs Saketh - 6 years, 5 months ago

Log in to reply

My argument is a little different, I model the situation like that since the disc is rotating with constant angular velocity, net energy imparted to the disc is zero.

So the net energy initially lost by the disc just when a ball just sticks to it.

E l o s t = 1 2 ( d m ) w R 2 {E}_{lost}=\frac{1}{2}(dm){wR}^{2}

And energy gained by the disc is equal to the potential energy lost by that ball from the point where it got attached to the disc to the point where it left the disc tangentially.

E g a i n e d = 2 ( d m ) g R c o s ( x ) {E}_{gained}=2(dm)gRcos(x)

Now E g a i n e d = E l o s t {E}_{gained}={E}_{lost} hence

2 ( d m ) g R c o s ( x ) = 1 2 ( d m ) w R 2 2(dm)gRcos(x)=\frac{1}{2}(dm){wR}^{2}

w = 2 g c o s ( x ) R w=2\sqrt{\frac{gcos(x)}{R}}

However our answers differ, what do you think about it @Mvs Saketh

Ronak Agarwal - 6 years, 5 months ago

Log in to reply

@Ronak Agarwal - sorry for late reply, i didnt recieve your comments notification for some reason, you see if you remember , theres a popular question about sand being dropped on a conveyer belt, and question is to find the heat loss, it turns out that as much heat is lost as heat as is obtained by kinetic energy , some thing similar happens here,

The actual energy loss by disc is dmw^2r and not its half,

incase you are not familiar with that conveyer belt question, or are unable to relate to it, then please tell, i will be glad to explain,

HINT- look at situation from discs frame as well to know the mysterious thing about the other half of energy,, where the balls appear to be coming at tangential velocity and then stopping losing all their kinetic energy as heat, even though in the lab frame all you see is frictional impulse pulling the balls along with the disc thus imparting it velocity

Basically system loses as much energy as heat as is imparted to each ball

Other than that you are perfectly correct,

such situations are called inherently inelastic processes, try as you might but you cant have 100% efficiency even theoretically, like chargeing a capacitor, or inductor,

Mvs Saketh - 6 years, 5 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...