A golden incircle
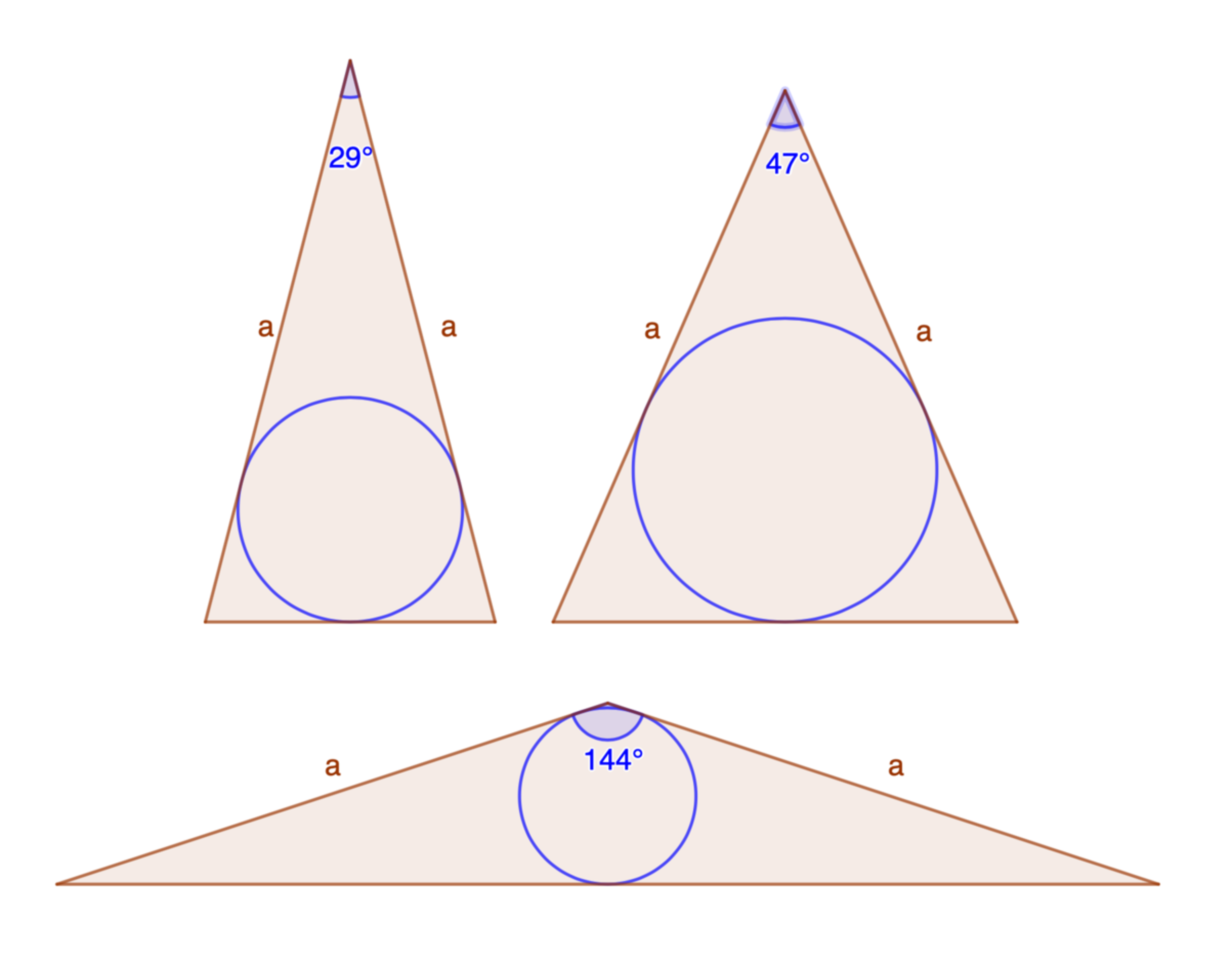
The figure above shows that three isosceles triangle with legs of the same length a but different apex angles produce incircles of different sizes. If the apex angle of the isosceles triangle that produces the largest incircle can be expressed as:
p sin − 1 ( s q + r ) ,
where p , q , r , and s are integers, with q being square-free, submit p + q + r + s .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
 Let the apex angle be
θ
=
2
x
,
0
<
x
<
2
π
.
Referring to the figure, triangles
△
A
I
N
and
△
A
C
M
are similar, hence
M
C
I
N
=
A
C
A
I
⇒
M
C
I
N
=
A
C
A
M
−
I
M
⇒
a
⋅
sin
x
r
=
a
a
⋅
sin
(
2
π
−
x
)
−
r
(
1
)
Without loss of generality, we take
a
=
1
, so from
(
1
)
we get:
sin
x
r
=
sin
(
2
π
−
x
)
−
r
⇔
r
=
sin
x
⋅
cos
x
−
r
sin
x
⇔
r
=
2
1
⋅
sin
(
2
x
)
−
r
sin
x
⇔
r
=
2
1
⋅
1
+
sin
x
sin
(
2
x
)
To maximise
r
we set
d
x
d
r
=
0
⇔
[
2
1
⋅
1
+
sin
x
sin
(
2
x
)
]
′
=
0
⇔
2
1
⋅
(
1
+
sin
x
)
2
2
cos
(
2
x
)
⋅
(
1
+
sin
x
)
−
sin
(
2
x
)
cos
x
=
0
⇔
2
cos
(
2
x
)
⋅
(
1
+
sin
x
)
−
sin
(
2
x
)
cos
x
=
0
⇔
2
(
1
−
2
sin
2
x
)
⋅
(
1
+
sin
x
)
−
2
sin
x
cos
2
x
=
0
⇔
sin
3
x
+
2
⋅
sin
2
x
−
1
=
0
⇔
(
sin
x
+
1
)
⋅
(
sin
2
x
+
sin
x
−
1
)
=
0
⇔
0
<
x
<
2
π
sin
2
x
+
sin
x
−
1
=
0
⇔
sin
x
=
2
5
−
1
The function
r
(
x
)
=
2
1
⋅
1
+
sin
x
sin
(
2
x
)
is concave down, since
r
′
′
(
x
)
=
−
(
1
+
sin
x
)
3
cos
x
⋅
(
3
sin
2
x
+
2
)
<
0
, for
0
<
x
<
2
π
,
hence, at the zero of
d
x
d
r
,
r
gets maximised.
This means that the incircle is the largest, when the apex angle is
θ
=
2
x
=
2
⋅
sin
−
1
(
2
5
−
1
)
.
For the answer,
p
=
2
,
q
=
5
,
r
=
−
1
,
s
=
2
, hence
p
+
q
+
r
+
s
=
8
.
Let the apex angle be
θ
=
2
x
,
0
<
x
<
2
π
.
Referring to the figure, triangles
△
A
I
N
and
△
A
C
M
are similar, hence
M
C
I
N
=
A
C
A
I
⇒
M
C
I
N
=
A
C
A
M
−
I
M
⇒
a
⋅
sin
x
r
=
a
a
⋅
sin
(
2
π
−
x
)
−
r
(
1
)
Without loss of generality, we take
a
=
1
, so from
(
1
)
we get:
sin
x
r
=
sin
(
2
π
−
x
)
−
r
⇔
r
=
sin
x
⋅
cos
x
−
r
sin
x
⇔
r
=
2
1
⋅
sin
(
2
x
)
−
r
sin
x
⇔
r
=
2
1
⋅
1
+
sin
x
sin
(
2
x
)
To maximise
r
we set
d
x
d
r
=
0
⇔
[
2
1
⋅
1
+
sin
x
sin
(
2
x
)
]
′
=
0
⇔
2
1
⋅
(
1
+
sin
x
)
2
2
cos
(
2
x
)
⋅
(
1
+
sin
x
)
−
sin
(
2
x
)
cos
x
=
0
⇔
2
cos
(
2
x
)
⋅
(
1
+
sin
x
)
−
sin
(
2
x
)
cos
x
=
0
⇔
2
(
1
−
2
sin
2
x
)
⋅
(
1
+
sin
x
)
−
2
sin
x
cos
2
x
=
0
⇔
sin
3
x
+
2
⋅
sin
2
x
−
1
=
0
⇔
(
sin
x
+
1
)
⋅
(
sin
2
x
+
sin
x
−
1
)
=
0
⇔
0
<
x
<
2
π
sin
2
x
+
sin
x
−
1
=
0
⇔
sin
x
=
2
5
−
1
The function
r
(
x
)
=
2
1
⋅
1
+
sin
x
sin
(
2
x
)
is concave down, since
r
′
′
(
x
)
=
−
(
1
+
sin
x
)
3
cos
x
⋅
(
3
sin
2
x
+
2
)
<
0
, for
0
<
x
<
2
π
,
hence, at the zero of
d
x
d
r
,
r
gets maximised.
This means that the incircle is the largest, when the apex angle is
θ
=
2
x
=
2
⋅
sin
−
1
(
2
5
−
1
)
.
For the answer,
p
=
2
,
q
=
5
,
r
=
−
1
,
s
=
2
, hence
p
+
q
+
r
+
s
=
8
.
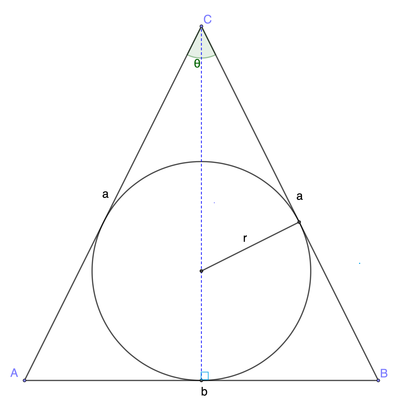 Image from Fletcher Mattox
Image from Fletcher Mattox
Let the apex angle and radius of the incircle be θ and r respectively. Then the area of the isosceles triangle is given by A △ = s r , where s = 2 2 a + 2 a sin 2 θ is the semiperimeter of the triangle. And the area of triangle is also given by A △ = 2 a 2 sin θ . Therefore 2 2 a ( 1 + sin 2 θ ) r = 2 a 2 sin θ ⟹ r = 2 ( 1 + sin 2 θ ) a sin θ . Since the larger the r the larger the incircle, the largest incircle occurs when 1 + sin 2 θ sin θ is maximum. Then d x d ( a 2 r ) = ( 1 + sin 2 θ ) 2 cos θ ( 1 + sin 2 θ ) − sin θ ( 2 1 cos 2 θ ) . Equating d x d ( a 2 r ) to zero, we have:
cos θ ( 1 + sin 2 θ ) ( 1 − 2 sin 2 2 θ ) ( 1 + sin 2 θ ) 1 + sin 2 θ − 2 sin 2 2 θ − 2 sin 3 2 θ 1 − 2 sin 2 2 θ − sin 3 2 θ sin 3 2 θ + 2 sin 2 2 θ − 1 ( sin 2 θ + 1 ) ( sin 2 2 θ + sin 2 θ − 1 ) = sin θ ( 2 1 cos 2 θ ) = sin 2 θ cos 2 2 θ = sin 2 θ ( 1 − sin 2 2 θ ) = 0 = 0 = 0
⟹ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ sin 2 θ = − 1 sin 2 2 θ + sin 2 θ − 1 = 0 ⟹ 2 θ = 2 3 π ⟹ sin 2 θ = 2 5 − 1 Not valid, since θ < π ⟹ θ = 2 sin − 1 ( 2 5 − 1 )
Therefore, p + q + r + s = 2 + 5 − 1 + 2 = 8 .
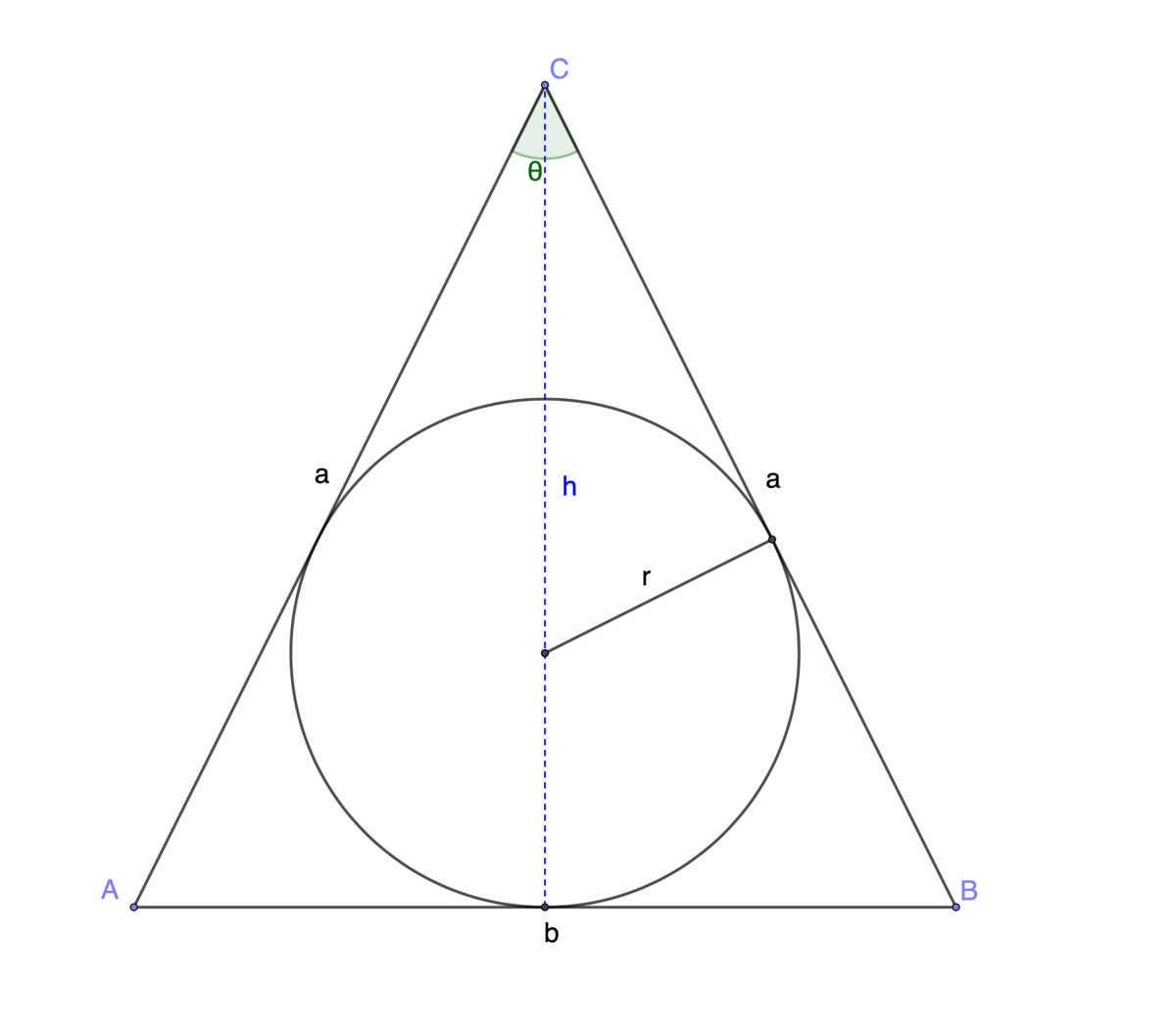
We want to express the inradius, r , as a function of the apex angle, θ . First find the area of the triangle.
A = 2 b ⋅ h = 2 1 ⋅ 2 a ⋅ sin 2 θ ⋅ a cos 2 θ = 2 1 a 2 sin θ
And the perimeter, P of the triangle. P = 2 ⋅ a + b
The inradius can be expressed as r = P 2 ⋅ A = 2 a + 2 a ⋅ sin 2 θ a 2 sin θ = 2 ( 1 + sin 2 θ ) a ⋅ sin θ
Now find extrema if any exist: d θ d r = 4 ⋅ ( sin 2 θ + 1 ) 2 2 ⋅ ( sin 2 θ + 1 ) ⋅ cos θ − sin θ ⋅ cos 2 θ = 0
Since the denominator is always positive, 2 cos θ ( sin 2 θ + 1 ) − sin ( θ ) cos ( 2 θ ) = 0
Let θ = 2 x ⟹ 2 cos 2 x ⋅ ( sin x + 1 ) − sin 2 x ⋅ cos x = 0
With some trigonometry, this can be reduced to a cubic in sin x :
sin 3 x + 2 sin 2 x − 1 = ( sin x + 1 ) ⋅ ( sin 2 x − sin x + 1 ) = 0
Taking each factor: sin x + 1 = 0 ⟹ θ = π , which can be ignored.
The quadratic factor, however, can be solved: sin x = 2 5 ± 1
Only the negative surd leads to a real root: θ = 2 x = 2 ⋅ sin − 1 ( 2 5 − 1 ) ≈ 7 6 . 3 4 ∘
So the required response p + q + r + s , is 2 + 5 − 1 + 2 = 8
@Fletcher Mattox , you have used a as side length as well as in the answer expression. I suggest to use a ′ in the answer expression.
I have changed them to p , q , r , and s . Change your solution. Note that r is negative.
@Chew-Seong Cheong does it look ok now?
@Fletcher Mattox , I have rearranged the three triangles so that they appear bigger for the details. Simplify the problem statement. Use ⋅ only when necessary. In this case it is not necessary. Notice that constant's name p is in italic but function's name sin is not in italic. Added "and" in " p , q , r , and s " just to make it more English-like. Note that r is negative, therefore I have removed "positive". "with q being " instead of "is", grammar.