A Golden Substitution
Given that x 2 = x + 1 , find the value of x 1 + x + 1 1
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Moderator note:
Nice. An alternative approach is x 1 + x + 1 1 = x 2 x + x + 1 1 = x + 1 x + x + 1 1 = x + 1 x + 1 = 1 .
At the point at which you get x 1 + x 2 1 , an even faster way is to notice that dividing x 2 = x + 1 by x 2 gives 1 = x 1 + x 2 1 which leads directly to the solution.
Doesn't compute. 1 squared=1 That equals 1+1=2. 1/1+1/2=1 1/2. How do you figure 1=2=1 1/2? Yes, one would have been my answer glancing at it but it doesn't work. Couldn't figure another answer that did.
Log in to reply
I am not solving for x but I am finding the value of the expression given instead. In fact there are two possible values of x ; 2 1 ± 5 .
It is given that: x 2 = x + 1 . Dividing throughout by x 2 , we have 1 = x 1 + x 2 1 . Since x 2 = x + 1 , then x 1 + x + 1 1 = x 1 + x 2 1 = 1 .
x 2 = x + 1 ⇒ x 1 + x + 1 1 = x 1 + x 2 1 = x 2 x + 1 = x 2 x 2 = 1 This doesn't account for the possibilities x = 0 or x = − 1 , so we need to check if they satisfy the original equation: 0 2 = 0 + 1 ( − 1 ) 2 = − 1 + 1
Just look at the question you will get the answer.
I didnt get it by looking -_-
When we proceed for (1÷x) + [1÷(x+1)], we get (2x + 1)÷(x^2 + x). Substituting numerator x + x + 1, we get x + x^2 {from given equation}. Thus numerator and denominator cancel each other out and we obtain result as 1.
Just simply take the LCM, 1/x + 1/(x+1) = (x+1+x)/x(x+1) = ( x^2 +x )/ x.x^2 = x(x +1)/ x.x^2 = 1
x²=x+1.now,x²-x=1.now,x(x-1)=1,now,x-1=1/x,now substituting in 1/x +1/x+1. We do ,(x-1)+1/(x+1). Solving it we get 1
x 2 = x + 1 ⇒ x = x x + 1 ⇒ x 1 = x + 1 x ⇒ x 1 = x + 1 x + 1 − 1 ⇒ x 1 = 1 − x + 1 1
⟹ x 1 + x + 1 1 = 1
x^{2}=x+1 -> x^{2}-x=1 -> x(x-1)= thus, x=1
1/x + 1/(x + 1) = 1/x + 1/x^2 = (x + 1)/x^2 = 1
This is the same as 1/x + 1/x^2 or x/x^2 + 1/x^2 or (x+1)/x^2 or x^2 over x^2 which is 1.
Well first I modified the first equation and factored it
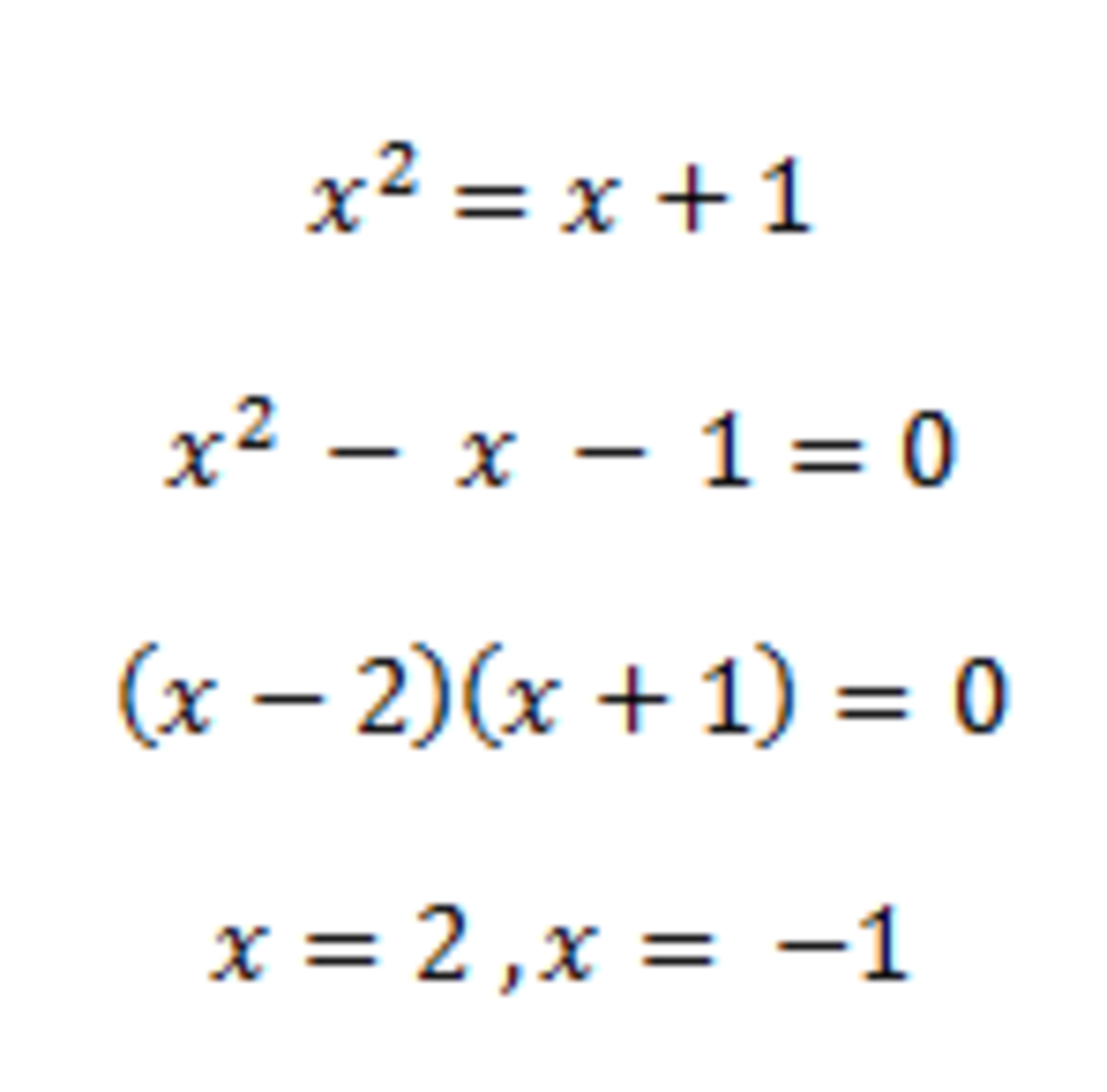
I got these results. I substituted -1 to x in the expression, however one of the denominators would be 0 making it undefined. So I substituted 2 to the expression and got this:
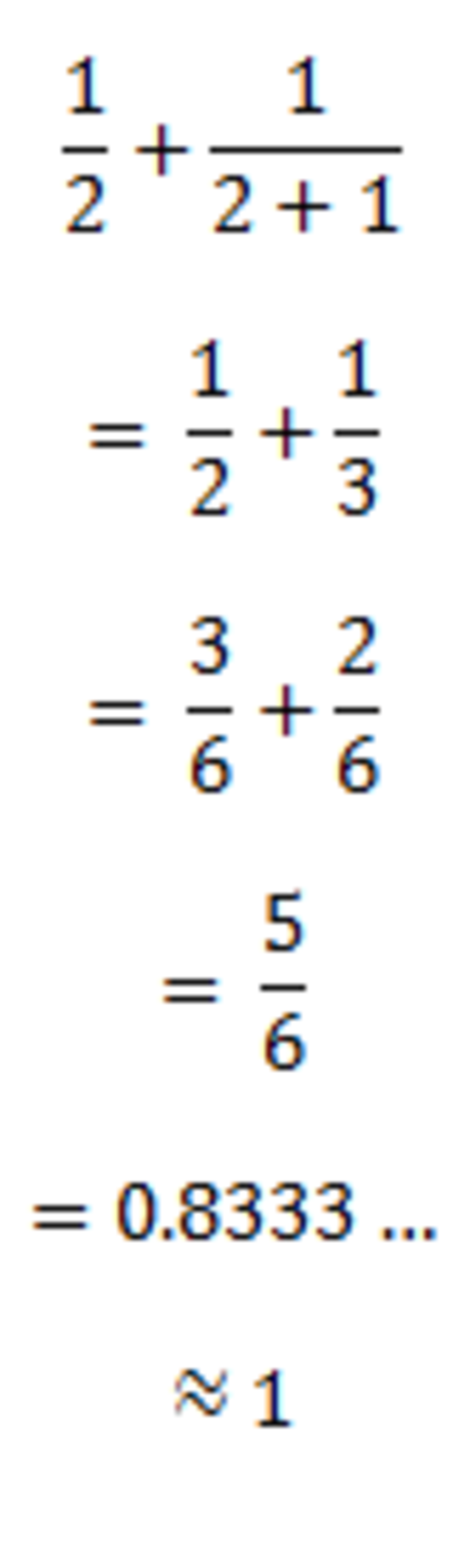
Since the answer should be an integer, I rounded it up and answered 1 rather than 0.83333.....
That's not a correct factorisation. ( x − 2 ) ( x + 1 ) = x 2 − x − 2
The answer is 1.
If x^2 = x + 1, then x^2 + x = x + 1 + x <=> x^2 + x = 2x + 1
So:
1/x + 1/(x + 1) = (x + 1 + x)/(x^2 + x) = (2x + 1)/(x^2 + x) =
= (2x + 1)/(2x + 1) = 1
What i did is to find like denominators, first. This obtains x 2 + x 2 x + 1 If you add x to both sides of the given, you get that x 2 + x = 2 x + 1 Thus, the answer is 1.
Since x 2 = x + 1 , x 2 + x = 2 x + 1 .
x 1 + x + 1 1 = x 2 + x 2 x + 1 = 2 x + 1 2 x + 1 = 1 .
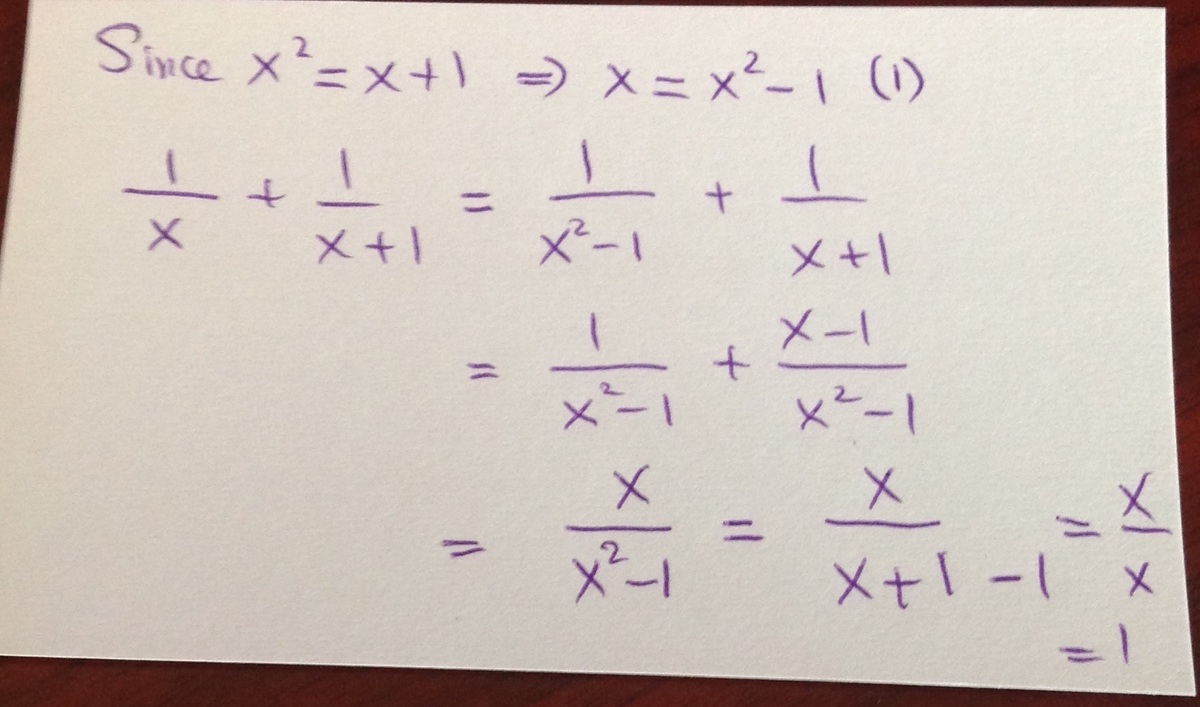
What I like about this is that you don't have to solve the quadratic! In fact, notice that by substitution: x + 1 1 = x 2 1 due to the given fact.
Now simplify: x 1 + x + 1 1 = x 1 + x 2 1 = x 2 x + 1
But remember that x 2 = x + 1 , so x 2 x + 1 = x 2 x 2 = 1