A geometry problem by Akshay Yadav

Geometry Level 5

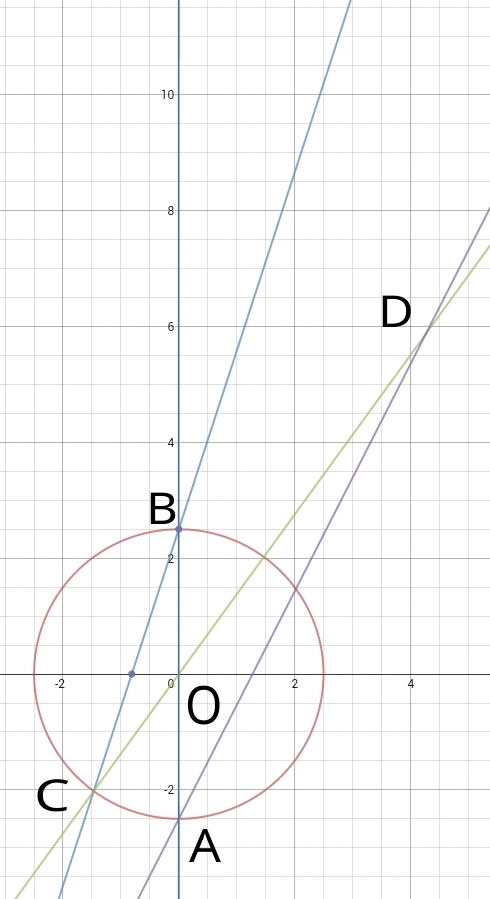
The figure represents above shows a Cartesian plane.

In the given figure $O= (0,0)$ is the center of a circle with radius $\dfrac{5}{2}$ units. $\angle ABC =18^\circ$ and $\angle ADC = 9^\circ$ .

If the $x$ -coordinates of $D$ are in form

$\dfrac{a(\sqrt{a}-b)(1+\sqrt{a}-\sqrt{ac+c\sqrt{a}})}{c^2(c-c\sqrt{a}+\sqrt{\frac{c}{a+\sqrt{a}}}+\sqrt{\frac{ac}{a+\sqrt{a}}}-c\sqrt{ac+c\sqrt{a}}+\sqrt{a}\sqrt{ac+c\sqrt{a}})}$

Note that $a$ , $b$ and $c$ are mutually prime positive integers.

Find $a+b+c$ .

You may use the fact that $\sin 18^\circ=\dfrac{\sqrt{5}-1}{4}$ .

Clarification : Angles are measured in degrees.

It is a challenge for all those who love geometry! This is the toughest problem that I have posted on Brilliant till now.

The answer is 10.

1 solution

Ariel Gershon
Mar 19, 2016

Since $O$ is the centre of the circle and $B$ is a point on the circle, we have $\angle AOC = 2\angle ABC = 36^{\circ}$ .

Since $\angle AOC$ is an external angle of $\triangle AOD$ where $\angle ADO = 9^{\circ}$ , then $\angle OAD = 36 - 9 = 27^{\circ}$ .

Therefore $\overline{COD}$ has equation $y = x \cot(36^{\circ})$ and $\overline{AD}$ has equation $y = x \cot(27^{\circ}) - \dfrac{5}{2}$ . Since the intersection of these two lines is $D$ , we just need to solve for $x$ : $x = \dfrac{5}{2(\cot(27)-\cot(36))}$ Now the hard part is equating this into the complicated form above. I won't post my entire derivation here because it's almost a page long. Here is the final answer: $x = \dfrac{5(\sqrt{5}-3)\left(1+\sqrt{5}-\sqrt{2(5+\sqrt{5})}\right)}{4\left( 2 - 2\sqrt{5} + \sqrt{\frac{2}{5+\sqrt{5}}} + \sqrt{\frac{10}{5+\sqrt{5}}} + (\sqrt{5}-2)\sqrt{2(5+\sqrt{5})} \right)}$

Therefore we get $a+b+c = 5+3+2 = \boxed{10}$ .

For the record, this expression has a much simpler closed form: $x = \dfrac{5\sqrt{10-2\sqrt{5}} + 10\sqrt{5}}{8}$

I had never thought that anyone would post a solution to this problem as it is extremely long, your solution is very good and appropriate. +1

Akshay Yadav - 5 years, 2 months ago

Thanks! I can't imagine how you came up with such a complicated expression. It was fun to solve though!

Ariel Gershon - 5 years, 2 months ago

Even I don't know how I ended up with that, I was merely playing the expression!😛

Akshay Yadav - 5 years, 2 months ago

A geometry problem by Akshay Yadav

It is a challenge for all those who love geometry! This is the toughest problem that I have posted on Brilliant till now.

The answer is 10.

1 solution

0 pending reports