A good rotational motion question!
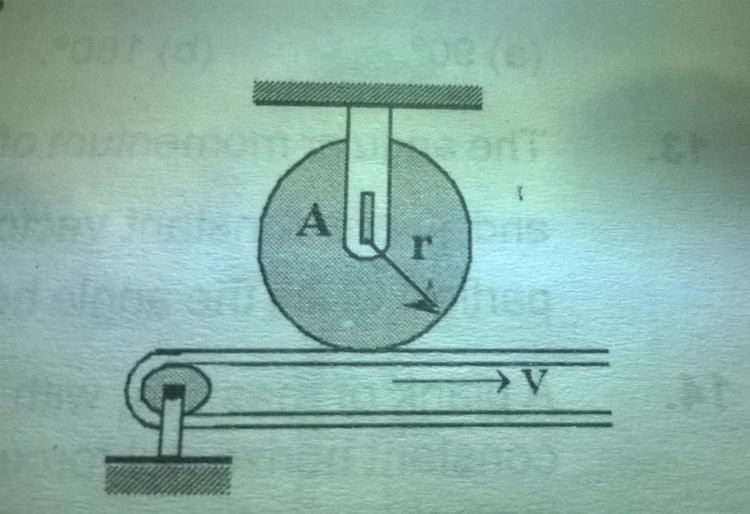 Disc A has a mass of 4 kg and a radius
r
=
7
5
mm ,it is at rest when it is placed in contact with the belt, which moves at a constant speed
v
=
1
8
ms
−
1
. Knowing that coefficient of kinetic friction is
u
k
=
0.25 between the disc and the belt , determine the number of revolutions executed by the disc before it reaches a constant angular velocity Assume that the normal reaction by the belt on the disc is equal to weight of the disc.
Disc A has a mass of 4 kg and a radius
r
=
7
5
mm ,it is at rest when it is placed in contact with the belt, which moves at a constant speed
v
=
1
8
ms
−
1
. Knowing that coefficient of kinetic friction is
u
k
=
0.25 between the disc and the belt , determine the number of revolutions executed by the disc before it reaches a constant angular velocity Assume that the normal reaction by the belt on the disc is equal to weight of the disc.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The disc will reach constant angular velocity when v = ω × r where r = r a d i u s o f d i s c , ω = a n g u l a r v e l o c i t y o f d i s c , v = s p e e d o f b e l t . Here kinetic friction will provide the torque. As we all know the equation τ = I × α and τ = r × F .
Now, F = μ k N
N = m g
I = 2 M r 2 ( F o r d i s c , M o m e n t o f I n e r t i a = 2 M r 2 )
Now equating r × F = I × α and substituting the values we get α = 6 6 . 6 7 r a d / s e c 2 .
Using the equation of rotational motion ω f 2 − ω i 2 = 2 α θ where ω i = 0 and ω f = r v
v = 1 8 m / s ( g i v e n ) , substitute the values of v , α , r in the rotational equation of motion to get θ = 4 3 1 . 9 7 r a d i a n s
Therefore No of revolutions = 2 π θ = 2 π 4 3 1 . 9 7 ≈ π 2 1 6
The solution assumes that the angular velocity "linearly" increases with time and "instantly" stop when its rim velocity reaches the belt velocity. That "discontinuous" slope seems aphysical. Perhaps there's more to it than what has been consdiered.