A grid walk

Let $P$ be point $(0, 0)$ and $Q$ be point $(5,5)$ . Note that any path from $P$ to $Q$ must pass through either $(2,3)$ or $(3,2)$ . There are $\dbinom{5}{2} = 10$ ways of getting from $(0,0)$ to one of those points, and $\dbinom{5}{2} = 10$ ways of getting from one of those points to $(5,5)$ . Thus, there are a total $2 \times 10 \times 10 = 200$ ways of getting to $Q$ from $P$ .

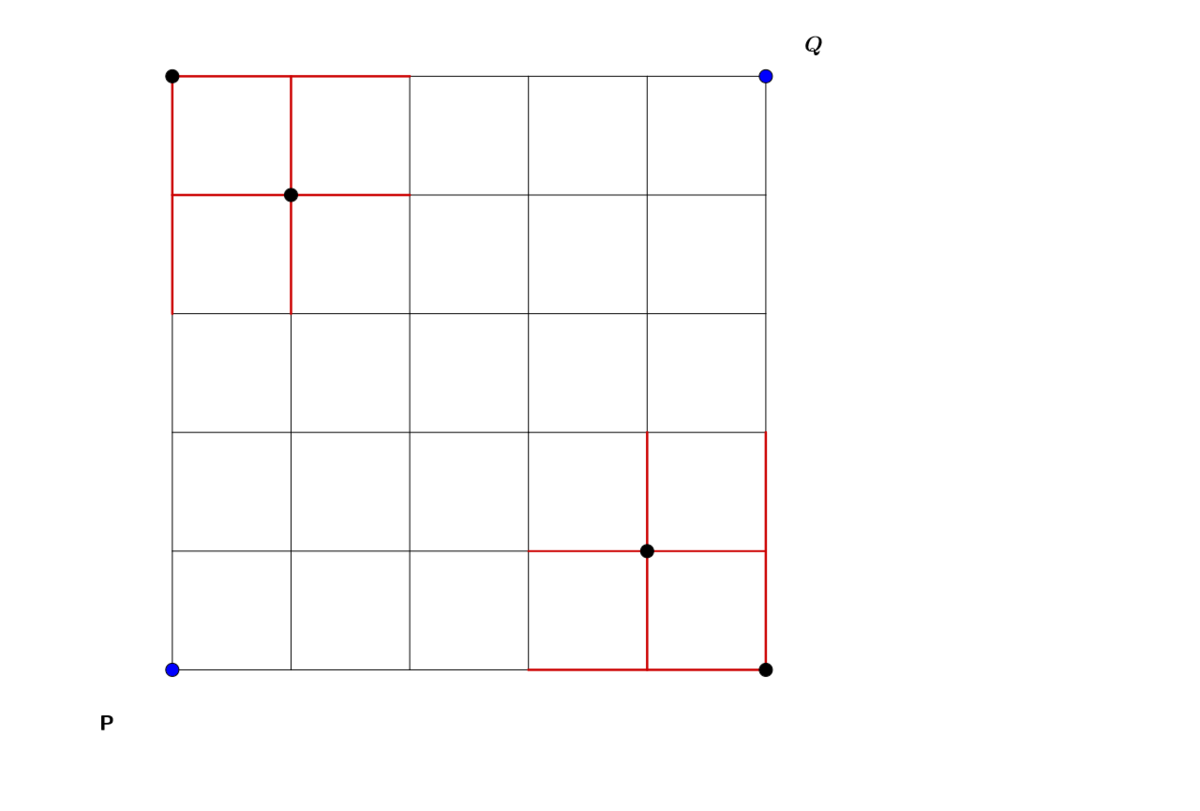
Let $P$ be point $(0,0)$ and $Q$ be point $(5,5)$

The total number of ways from $P$ to $Q$ on a complete grid is given by $\dbinom{10}{5}=252$

However here we have portions of the grid removed (denoted by red lines).Consider the upper left removed portion,any path from $P$ to $Q$ involving a red line would pass through exactly one of the black points( $(1,4)$ and $(0,5)$ ) in the region.

no of paths through $(1,4)$ is given by $\dbinom{5}{4}\times\dbinom{5}{1}=25$

no of paths through $(0,5)$ is given by $\dbinom{5}{0}\times\dbinom{5}{5}=1$

thus total number of paths involving red lines in upper left region is $(25+1)=26$

similarly we have $26$ paths involving red lines in lower right region,

Thus total number of valid paths from $P$ to $Q$ is given by $252-(26+26)=\boxed{200}$