A Handshake for Peace!

Probability Level 1

In the opening ceremony of the 2014 FIFA World Cup Brazil, all football teams who participates gathered together. The team captain of each team was handshaking with one another to promote their new act for world peace which was called "A Handshake for Peace!". Each team captain is as polite as the other. How many teams are there if there were a total of 595 handshakes?

Note: Each team captain had handshake with another team captain only once.

33 37 39 35 31

12 solutions

Charles Dutertre
May 24, 2015

There are $n$ captains. Take one, he shakes $n-1$ hands. Then take a second one, he has $n-2$ hands to shake because he already shook hands with the first one. etc... Therefore there will be $\sum_{k=1}^{n-1}k = \frac{n(n-1)}{2}$ handshakes, resulting in $n = 35$ .

simple one. I too did the same way!

santhosh muthyala - 6 years ago

Nice application of Gauss's Trick. You can also use the traditional formal $n(n+1)/2=595$ , which gives n=34, but then you need to add 1 since the the last coach did not shake hands with anyone (everyone shook his hand), so you get 35.

Scott Ripperda - 6 years ago

well it is the same, just took $n-1$ instead of $n$ . It is still the 'traditional' formula.

Charles Dutertre - 6 years ago

Jason Tenebroso
May 24, 2015

Let's assume that each team captain is a point. (In this case, let's assume there are 4 teams)

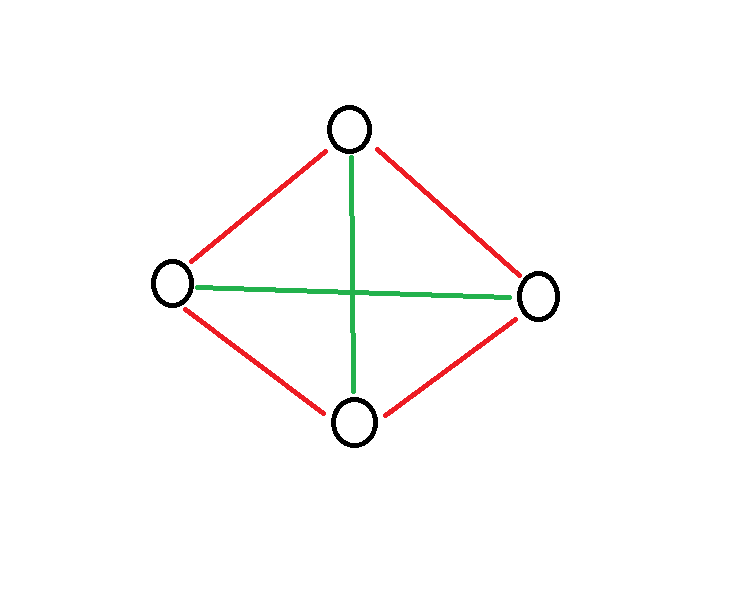
Notice that if we connect those points with one another, then we can create a polygon with a diagonal. the red segments above represents the side of a convex polygon, while green segments represents the diagonals . Furthermore, each segment(both green and red) that was formed by connecting those points represents the handshakes of team captains with one another. Therefore, the total handshakes are the sum of the sides and diagonal of the polygon. This analysis will lead us to a general formula.

let n=number of sides of a polygon " S=total handshakes

S=n + ((n/2)(n-3) therefore; S=(n^2-n)/2

substitute; 595=(n^2-n)/2 n^2-n-1190=0 n=35 and n=-34

since, the number of handshake cannot be negative, and the number of sides of a polygon is always equal to the vertices which represents team captains, so the answer is 35.

Or you can simply use combinations. The number of teams is equal to the number of captains (say $n$ ) and every two of them handshakes only once. So, the number of handshakes can also be interpreted as the number of two distinct element subsets of a set of $n$ (distinct) elements which is simply $\binom n2$ . Since it is given that there are $595$ handshakes, you have,

$\binom n2=595\implies \frac{n(n-1)}{2!}=595\implies n^2-n-1190=0$

Using quadratic formula, the only positive integral solution to the above quadratic equation is $n=35$ which is our answer.

Note: There's also a quick alternative. Compute $\sqrt{1190}$ first which is approximately $34.496$ . Now, try the product of two consecutive integral values around this value and you'll see that $35\times 34=1190$ giving us $n=35$ . This actually uses the fact that $n(n-1)\approx n^2$ for large enough $n$ .

Prasun Biswas - 6 years ago

Or. You notice that $1190$ ends in a 0. Hence the only solutions must be either 35 or 39. 39 is obviously (?) too large , hence answer is 35.

Jihoon Kang - 6 years ago

Isn't that Neymar and Pique?

Rifath Rahman - 6 years ago

Brock Brown
May 24, 2015

Python 2.7:

def goal(captains):
    return (captains*(captains-1))/2.0 == 595
captains = 1
while not goal(captains):
    captains += 1
print "Answer:", captains

Daniel Dorinbaum
Jun 1, 2015

I just added 1-33 and that was too low and added 34 to the past total and it was the answer so 35 since they can only handshake the same team once

Jack Sweeney
May 30, 2015

The easy way to solve this is (as you have multiple answers). 35 is the only one that can go into 595 as a whole. Unless you want 0.2 of a hand shake. It's not very fulfilling though

Nicholas Spinner
May 28, 2015

Cheater Solution:

Divide 595 by each possible answer.

35 is the only answer where the division is a whole number.

Brendan Warner
May 28, 2015

595*2=1190 sqrt(1190)=34.5 or 35

Moderator note:

Why? What are you doing here? Random Math?

Intuition, math isn't random

Brendan Warner - 6 years ago

Shawn Pereira
May 28, 2015

Here's how I did:

Let x be number of captains (=number of teams)

Total handshakes =[( x )( x -1)]/2

595 = [( x )( x -1)]/2

1190 = [( x )( x -1)]

1190 = { x }^{ 2 } - x

{ x }^{ 2 } - x -1190 = 0

Therefore, x = 35 and -34 (discarded)

Therefore there are 35 teams/captains.

Samuel Prasetya
May 27, 2015

use a combination xC2 = 595

Aritro Paul
May 26, 2015

The solution will be n*n+1/2=595. n will be 34. Since,captain of n will have n-1 handshakes, no of teams will be 35

Paulo Victorio
May 26, 2015

Trial and Error works best here. Whichever option that results to a whole number (since we're talking about a real situation here) will be the answer.

Aqeel Madhi
May 25, 2015

I dd it the old Fashioned Long way!Trial and Error,while it may be rudimentary it still worked!35X17=395!

A Handshake for Peace!

12 solutions

Moderator note:

0 pending reports