A Harmonic Hex
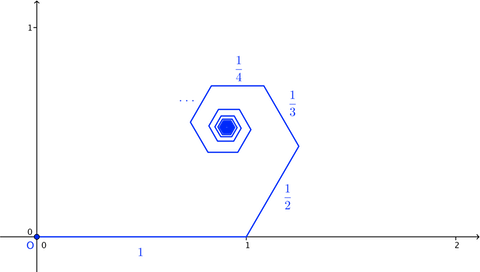 The image above shows a
broken line
(a series of connected line segments) starting at the origin,
O
. The
n
th segment in the broken line has length
n
1
, and at the end of each segment, the broken line turns
6
0
∘
counter-clockwise.
The image above shows a
broken line
(a series of connected line segments) starting at the origin,
O
. The
n
th segment in the broken line has length
n
1
, and at the end of each segment, the broken line turns
6
0
∘
counter-clockwise.
As the number of segments in the broken line approaches infinity, the final endpoint of the broken line approaches a point P . The distance OP can be written as b a π , where a and b are positive coprime integers. Find a + b .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Beautiful!!!!!!!
awesome solution
u did it so beautifully! great!
Wow. Good job.
I did something similar but found it difficult to complete / interpret the problem geometrically :
If we start at (1,0) and call the basic rotation (pi/3) (e^i * pi/3 in terms of complex numbers), we get
x + 1/2x^2 + 1/3x^3 + .... infinity
= $1 + .x + x^2 +...
= $1dx/(1-x)
(Of course, i am assuming that the infinite series converges since |x| <=1 )
= -ln (1-x)
= -ln(1-e^ipi/3)
Now, i am assuming that since it is difficult to handle it algebraically, we have to use geometric intuition.
So the above becomes -ln(1-cos(pi/3),-sin(pi/3))
= -ln(1/2,-sqrt(3)/2)
= -ln((1)e^i(-pi/3)) expressing above as r*e^ithera = -ln 1 - ln(e^-ipi/3))
= 0 -(-ipi/3)
= i*pi/3
That seems to represent a point that is pi/3 above our starting point (1,0) but we have to find distance from O and so it will be sqrt(1 + (pi/3)^2)
but this does not seem to result in integral ratios
Anything wrong with the above interpretation ?
Log in to reply
Possibly, this represents some kind of phase extraction ??
So what are the co-ordinates of the point ?
Nice solution!
I would clap, but I wore my hands into stumps doing this the silly way. Well done.
Very nice. I did it exactly the same way.
sick problem but beautiful at the same time
good god.... thid is sooo good!! loved it! :>
I did not understand that part, about the taylor expansion for ln(1+x)
I did the same too !!!
Did the same! Absolutely delectable...
we can do this problem by taking a segment as a vector or complex number we know that the sum of all such complex numbers of vectors will give by vector addition the vector joining origin and the approaching point. Any general segment when moved parallel so that it passes through the origin with same magnitude can be represented by
Z = r 1 e i ( r − 1 ) π / 3 so the addition of all such complexes is given by 1 ∑ ∞ Z = r 1 e i ( r − 1 ) π / 3 = 3 π
Let the n th segment be represented by a complex number u n . For example, u 1 = 1 , u 2 = 2 1 e i 3 π , u 3 = 3 1 e i 3 2 π , ... u n = n 1 e i 3 n π . Then the coordinates of the end of the n th segment is given by P n ( ℜ ( z n ) , ℑ ( z n ) ) , where z n = ∑ k = 1 n k 1 e i 3 ( k − 1 ) π . Then the distance from the origin O P n = ∣ z n ∣ . Then we have:
n → ∞ lim z n = k = 1 ∑ ∞ k e i 3 ( k − 1 ) π = e − i 3 π k = 1 ∑ ∞ k e i 3 k π = e − i 3 π ln ( 1 − e i 3 π ) = e − i 3 π ln ( 1 − 2 1 − i 2 3 ) = − e − i 3 π ln ( 2 1 − i 2 3 ) = − e − i 3 π ln ( e − i 3 π ) = i 3 π e − i 3 π
Therefore, O P = ∣ ∣ ∣ n → ∞ lim z n ∣ ∣ ∣ = ∣ ∣ ∣ i 3 π e − i 3 π ∣ ∣ ∣ = 3 π ⟹ a + b = 1 + 3 = 4 .
The position of P as a complex number can be written as :
1 + e^(i pi/3)/2 + e^(2 i pi/3)/3 +...... which is of the form sum (from n = 1 to infinity ) [x^n / n] (where x = e^i pi/3. ) = sum (from n = 1 to infinity ) [x $x^(n-1)dx] = x $ 1 dx / (1-x) (bringing the infinite series summation inside = - x ln | 1 -x | = - e^(i pi/3) ln | 1 - e^(i pi/3) | Using eulers formula and separating the real and imaginary parts, we get x coordinate of P = pi/6, y coordinate of P = sqrt(3) pi / 6
Using euclidean distance formula, the distance of p from the origin = sqrt [ pi^2/36 + 3pi^2/36] = sqrt[4pi^2/36] = pi /3, thus giving 4 as the required answer
Let ( x , y ) be the coordinates of P . It is easy to see that x = n = 0 ∑ ∞ n + 1 cos n θ y = n = 0 ∑ ∞ n + 1 sin n θ where θ = 3 π . Instead of trying to find these sums directly, let's exploit complex numbers. Consider x + i y = n = 0 ∑ ∞ n + 1 cos n θ + i sin n θ = n = 0 ∑ ∞ n + 1 e i n θ Let z = e i θ , then we have n = 0 ∑ ∞ n + 1 z n = − z ln ( 1 − z ) That last step comes from the Taylor expansion for ln ( 1 + x ) about x = 0 . Note that z = cos θ + i sin θ = 2 1 + i 2 3 .
Now, − z ln ( 1 − z ) = − z ln ( 2 1 − i 2 3 ) = − z ln e − i 3 π = i z 3 π = x + i y Taking the modulus of both sides, and noting that i z has modulus 1 we arrive at x 2 + y 2 = O P = 3 π .