An Original Heptagonal Problem
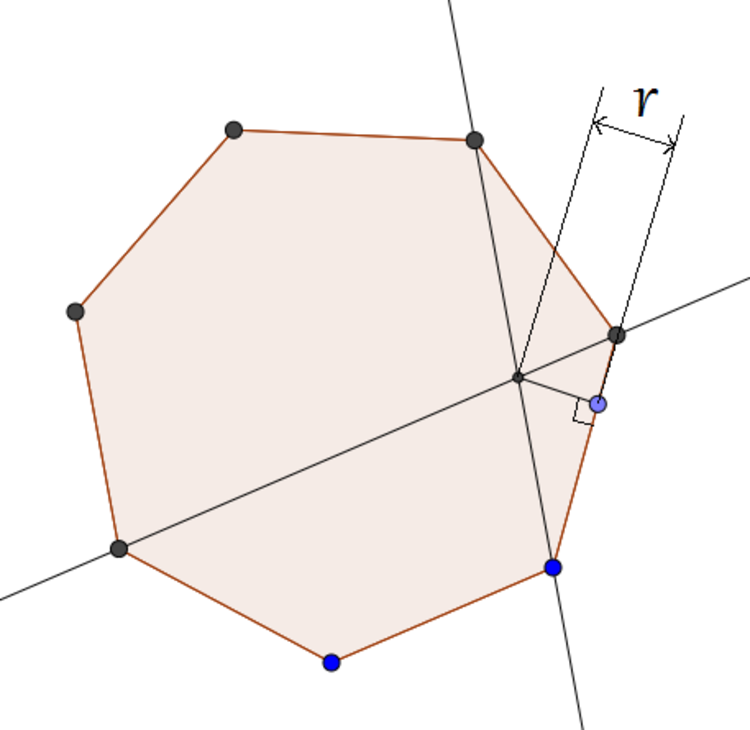 Consider the above construction on a regular heptagon where the distance of the point of intersection of the indicated diagonals from the indicated edge is called
r
. Also, consider the
scalene
triangle (not shown) whose vertices are some suitably chosen three vertices of the same regular heptagon. Let its inradius be called
R
. What is the ratio
R
:
r
?
Consider the above construction on a regular heptagon where the distance of the point of intersection of the indicated diagonals from the indicated edge is called
r
. Also, consider the
scalene
triangle (not shown) whose vertices are some suitably chosen three vertices of the same regular heptagon. Let its inradius be called
R
. What is the ratio
R
:
r
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Oh well, I hadn't noticed this! The most obvious solution. Kudos! I must admit, I had discovered the result in the complex way that my solution proceeds along, not noticing this rather intuitively obvious way. The difficulty level now needs to be reduced!
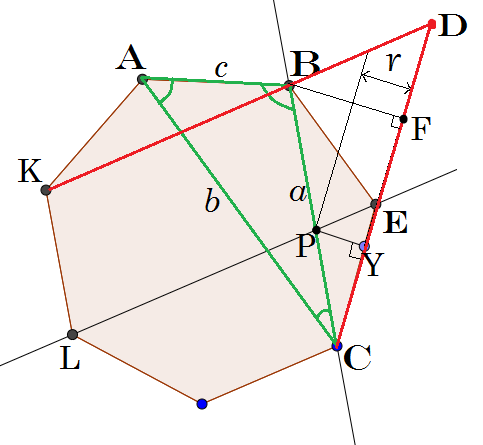
I am going to use a result that is easy enough to prove so it is fair to leave it to the readers. Refer to the first problem that appeared in INMO 1992, a very handy result useful in several places, (also in the ninth problem of the same paper!) here
C o n s t r u c t i o n
Note in the figure that Δ A B C is one such scalene triangle. Any other scalene triangle will be congruent to it, so which triangle is worked on is irrelevant. This one eases discussion. The sides are labelled as usual with uncapitalized letters and diagonal K B meets edge C E upon extension at D . B F is the perpendicular dropped on C D .
P A R T 1:
Consider triangles A B C and D B C . ∠ A C B = ∠ D C B (Angles subtended by equal chords (edges) A B and B E on a point on the circumference of the polygon, namely C . Equal chords subtend equal angles on the circumference. In this case, each of these is in fact 7 π radians) ∠ A B C = 7 4 π , can be seen as a sum of angles subtended at B by four equal chords. ∠ K B C = 7 3 π , can be seen as a sum of angles subtended at B by three equal chords. ⟹ ∠ D B C = π − ∠ K B C = 7 4 π So, ∠ A B C = ∠ D B C . These with the common side BC imply congruency of triangles:
Δ A B C ≅ Δ D B C .
Let us call the altitude on side b from vertex B of triangle A B C , h b . Note that, due to congruence, B F = h b . P Y is parallel to B F , so triangles C P Y and C B F are similar. This implies: B F P Y = C B C P . Consider the diagonal of the heptagon L E : It is of course parallel to the diagonal K B . So, P E is parallel to B D which means triangles C P E and C B D are similar. This implies: C B C P = C D C E . Together, we get: B F P Y = C D C E . But note that, C E is the same length as A B (as the heptagon is regular and edges are equal), i.e. c and C D = C A = b due to the congruence of triangles proved above. Using notations described,
h b r = b c ⟹ r = b h b × c
P A R T 2:
Now, we come to the inradius, R . Note that in Δ A B C , ∠ A B C = 7 4 π , ∠ B A C = 7 2 π , ∠ B C A = 7 π
Since, ∠ B is twice ∠ A , using the result at the top,
b 2 = a 2 + a c
Since, ∠ A is twice ∠ C , using the result at the top,
a 2 = c 2 + c b
Substituting, the second relation in the first, we get, with s as semiperimeter:
b 2 = c 2 + c b + a c = c ( a + b + c ) = 2 c s
Now, since inradius R is given by s Δ , where Δ is the area, and Δ may be written as 2 b × h b , we get, s = 2 R b × h b . Substituting,
b 2 = R c × b × h b ⟹ b = R c × h b
⟹ R = b h b × c .
Hence the conclusion.
I will be referring to Aditya's labelling.
Consider scalene triangle Δ A C E . The incentre of a triangle lies on the intersection of the angle bisectors. The angle bisector of ∠ A C E is C B , as B lies on the mid-arc of A E , and for ∠ C E A it is E L , by the same argument.
(This is so as A B = B E and therefore the angle subtended by the arcs are of equal value. Therefore ∠ A C B = ∠ B C E . This can be applied to the other case.)
Therefore, the intersection point of the question (point P ) is the incentre of Δ A C E , and by definition the inradius must be r , as E C must be tangential to the incircle.