A hint for my previous problem.

I saw that a lot of people have got my recently posed problem Rotating rod in magnetic field wrong. I believe they have answered $0$ . One gets $0$ if he assumes magnetic field constant in whole region inside metallic ring(in red) having radius $a << r$ . The same image is uploaded again :

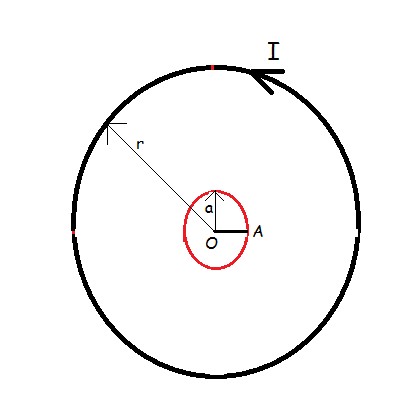
Actually, the magnetic field changes its value, and its expression can be obtained by aproximations. The magnetic field at a distance x from center ( $x <<r$ ) can be written as $B \approx B_{0} \bigg(1+ \dfrac{k}{2} \bigg(\frac{x}{r} \bigg)^n \bigg)$ , where $B_0$ is magnetic field at center( $O$ ) of the circular current carrying loop. Find $k+n$ .