A hole in the sphere - Part 3
A sphere of radius has a cylindrical hole drilled through it. The radius of the hole cylinder is , and its axis is a distance of away from the center of the sphere. This is depicted in the figure below. If , find the surface area of the hole (shaded in yellow).
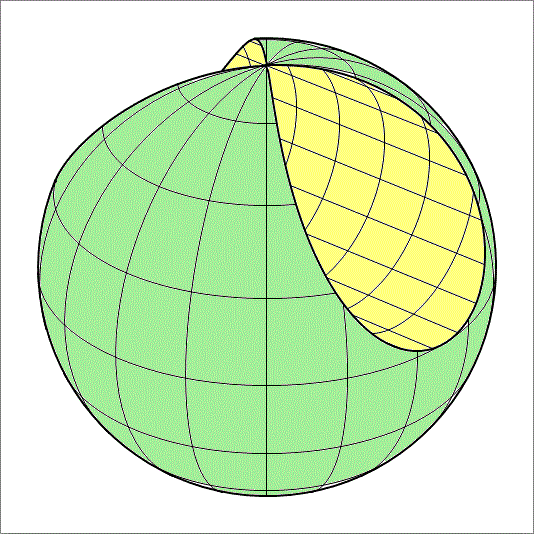
The answer is 400.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us attach a reference frame to the hole, with its origin at the midpoint of the two intersections of the axis of the hole cylinder and the sphere. Let's choose the z -axis to be along the axis of the hole cylinder, and the y -axis to point vertically up, passing through the center of the sphere at y = − 2 R , and this also determines the x -axis.
To find the area of the hole (yellow area), we'll move on the boundary of the hole in the x y plane, which is a circle of radius 2 R , and find the z coordinate of the intersection of the hole with the sphere. This is given by
z = R 2 − ( 2 R + 2 R sin ϕ ) 2 − ( 2 R cos ϕ ) 2
where 0 ≤ ϕ < 2 π . Simplifying the above expression, we obtain,
z = 2 R 2 ( 1 − sin ϕ ) = 2 R 1 − sin ϕ
Let ψ = 2 π − ϕ , then
z = 2 R 1 − cos ψ
Now, we can use the fact that sin 2 x = 2 1 ( 1 − cos ( 2 x ) ) , to write the above as,
z = R ∣ sin 2 ψ ∣
So that, the area integral is,
A = ∫ 0 2 π 2 ( 2 R ) z ( ψ ) d ψ = R 2 ∫ 0 2 π ∣ sin 2 ψ ∣ d ψ
Applying a change of variable, u = 2 ψ , results in,
A = = 2 R 2 ∫ 0 π ∣ sin u ∣ d u = 2 R 2 ∫ 0 π sin u d u = 4 R 2
Substituting R = 1 0 , gives us, A = 4 0 0 .