A hole in the sphere
A solid sphere of radius 2 0 has a cylindrical hole drilled through it. The radius of the hole cylinder is 1 0 , and its axis is 1 0 units away from the center of the sphere. This is depicted in the figure below. What percent of the sphere volume has been drilled out?
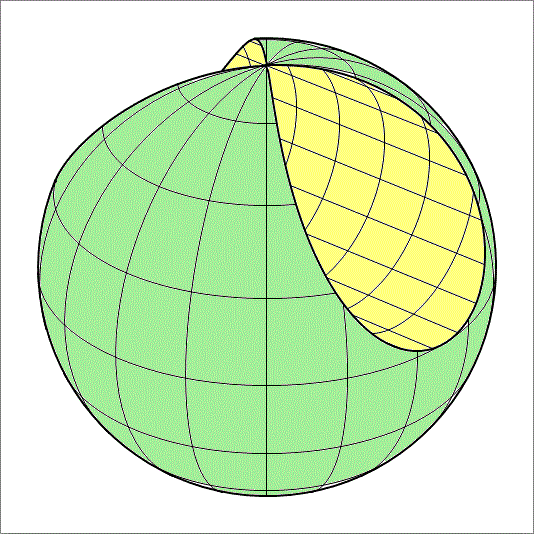
Note: It is possible to obtain the exact percentage by finding the exact value of the drilled out volume.
The answer is 28.78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
First, let's scale down by a factor of 1 0 in each direction. This makes the algebra neater and doesn't affect the percentage result.
By placing the centre of the sphere at the origin and the axis of the cylinder on x = 1 , we have the equations x 2 + y 2 + z 2 = 4 for the sphere and x 2 − 2 x + y 2 = 0 for the cylinder.
It's easier to work in cylindrical coordinates r , ϕ , z , in which x = r cos ϕ and y = r sin ϕ ( z is unchanged).
The sphere now has equation r 2 + z 2 = 4 , and the cylinder r 2 − 2 r cos ϕ = 0 , or (almost) equivalently r = 2 cos ϕ .
We have V = 2 ∫ 0 π ∫ 0 2 cos ϕ 4 − r 2 r d r d ϕ = ∫ 0 π 3 1 6 ( 1 − sin 3 ϕ ) d ϕ = 9 1 6 ( 3 π − 4 )
The volume of the sphere is 3 3 2 π ; so the required percentage is 1 0 0 × 3 3 2 π 9 1 6 ( 3 π − 4 ) = 1 0 0 × 6 π 3 π − 4 ≈ 2 8 . 7 7 9 %
Excellent solution. Thanks for sharing it.
Commented solution code is attached. Results are printed at the end. The answer comes out to around 2 8 . 8 %