A Game of Murderers
Imagine that there is a group of ruthless murderers. They play a game. The game was about killing people. The murderers make a circle. One murderer starts first. He kills the next person who is not dead. The rest (who are not dead) do the same. The game stops when only one person is alive (the winner).
This is a example of murderers playing
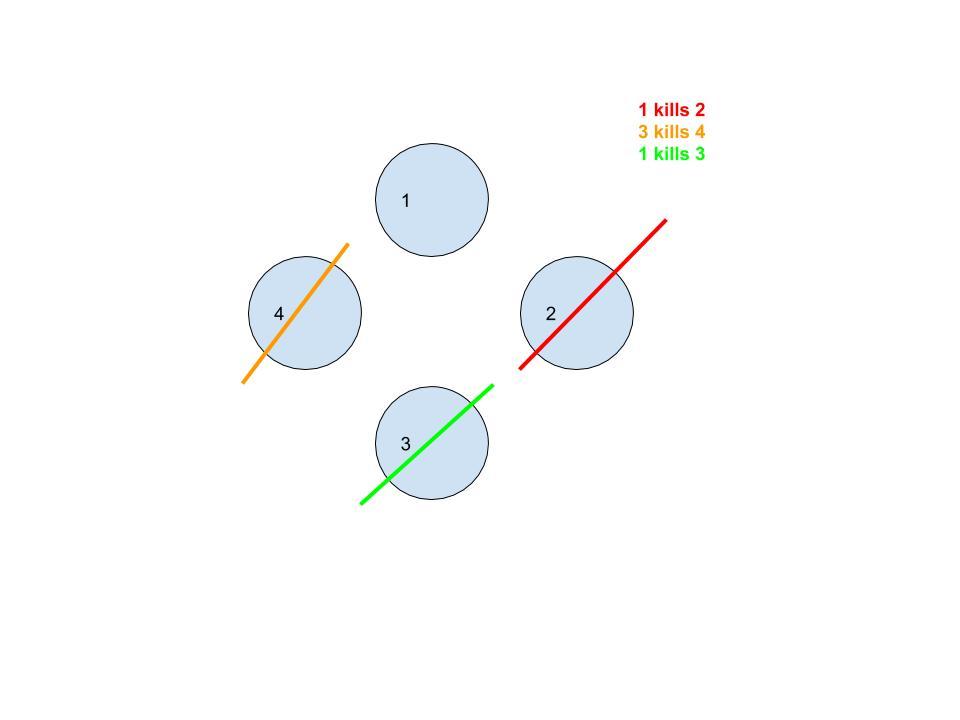
Who will win if there are 101 murderers?
Hint: think of if x is a whole number.
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
When total number of murderers is of the form 2^p, the winner position is 1, and then the position increases by 2 units for increase in the total number by 1 until it becomes of the form 2^(p+1). Since 101=2^6+37, therefore the winning position is 1+(37)(2)=1+74=75