Grooves through a sphere

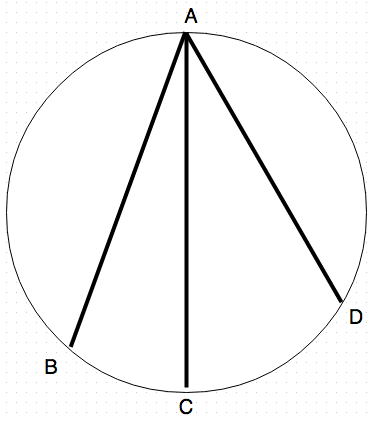A sphere, as shown in the image is placed on a horizontal surface with three grooves drilled into it from point $A$ to points $B, C,$ and $D.$

$\overline{AC}$ is a diameter to the sphere, while $\overline{AB}$ and $\overline{AD}$ are chords, such that:

$\begin{aligned} \angle BAC &= \theta\\ \angle DAC &= 2\theta. \end{aligned}$

An object of mass $M$ is dropped thrice, each time through each groove, and the time taken for it to emerge out of the groove is measured.

Now, let $a:b:c$ (where $a,b,$ and $c$ are coprime integers) be the ratio of the respective times that the object takes to exit through grooves $\overline{AB}\,$ $\overline{AC}$ and $\overline{AD}.$ Find $a+b+c.$

Details and Assumptions

• Gravity is constant at $g = 9.8\text{ m/s}^2$ vertically downwards at all times.
• The grooves have negligible friction, and the object is considered to be point sized.

Please do note that this problem was taken from a teacher of mine.