A King's problem
Once again, the great and mighty King of Swadia, absolute ruler of his kingdom, is bored. In such moments, the King tends to annoy his advisers with bunch of hard and unnecessary problems. For today, King made quite a nice problem. He will give two number, first , then , and he wants to know two last digits of number .
Of course, the King will give more such pairs and he wants a solution to all of them. The first man who will accomplish this task, will be given a lot of gold, mead and some other privileges.
However, a smart man named Billy already solved this, so he gets all the privileges. But if You correctly solve this task, you will earn certain amount of brilliant points.
Input:
Input is done through file "King.txt" . First number represents how many questions will be. Question is asked with two numbers, first number , then . Answer to such question is . Find the sum of all such answers.
Some details and guarantees:
- In each question, numbers will be taken from .
- There will be no questions which will ask for
- File can be downloaded from here , as well.
Example:
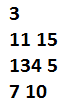
Questions:
Questions related to this problem can be asked here .
The answer is 3714210.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
When confronted with a problem similar to this, I find it very helpful to put the code aside at first and just focus on the mathematical aspects. I used knowledge of exponents in order to solve this problem. First, I determined which digits in integer number A determined the last two digits of A B , or A B m o d 1 0 0 . After a little bit of math, I determined that only the last two digits of number A affected the last two digits of A B .
The idea behind this was that any integer number can be re-written as the sum of its components. For instance, 3 4 7 can be rewritten as 3 0 0 + 4 7 , and we know that 3 4 7 2 is the same as ( 3 0 0 + 4 7 ) 2 . Since 3 0 0 has two zeros as its last two digits, we know that multiplying it by any integer will result in a number whose last two digits are also zeros. This shows us that when raising 3 4 7 to a power, any numbers before the 4 7 are irrelevant when determining the last two digits of the result. This idea can be expanded and applied to any integer and any digit.
Now that I know this, I only need to work with the last to digits of A to get my answer. But where do I go from here? The B value is still terribly large.
Through laws of exponents, we know that A B = A C ∗ A C for C = B / 2 since 2 C = B and A C ∗ A C = A C + C + A 2 C . If B is odd, we can easily account for this by decreasing B by one to make it even and then accounting for this later by multiplying A C ∗ A C by A (this adds one to the exponent.) We've now finished all of the mathematical aspects of this problem. Now we just have to put it into code.
Please ask any questions if any of my explanation is not clear, this is my first time writing an explanation. My program uses a recursive method to find the last two digits of A B . note: Make sure to include import java.util.*; at the top of your program.