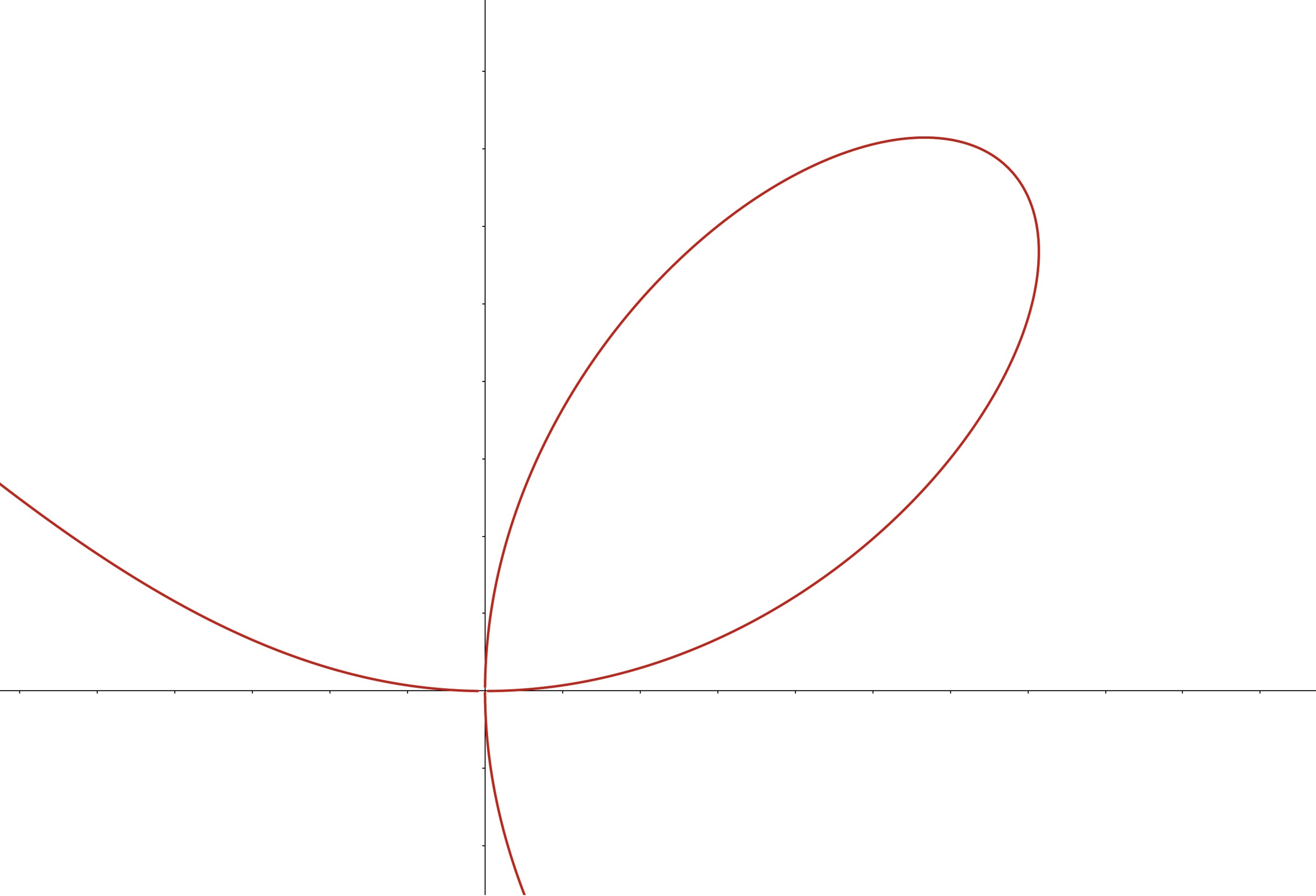
A leaf with an inscribed square

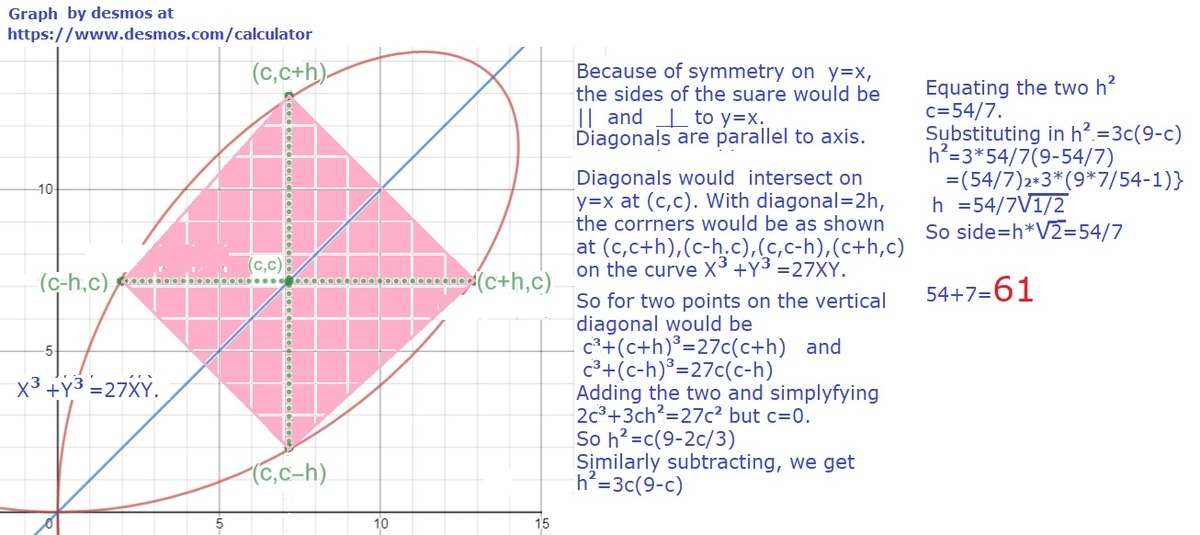
Applying the transformation $x = x' \cos 45° - y' \sin 45°$ and $y = x' \sin 45° + y' \cos 45°$ rotates the leaf $45°$ and gives it a new equation of $(\frac{\sqrt{2}}{2}x - \frac{\sqrt{2}}{2}y)^3 + ((\frac{\sqrt{2}}{2}x + \frac{\sqrt{2}}{2}y))^3 = 27((\frac{\sqrt{2}}{2}x - \frac{\sqrt{2}}{2}y))((\frac{\sqrt{2}}{2}x + \frac{\sqrt{2}}{2}y))$ , which rearranges to $y = \pm \sqrt{\frac{x^2(2x - 27\sqrt{2}}{-3(2x + 9\sqrt{2}}}$ .

Let the points of the inscribed square be $P(a, c)$ , $Q(b, c)$ , $R(b, -c)$ , and $S(a, -c)$ . Then by the properties of a square, $b - a = 2c$ , and since $P$ and $Q$ are on the equation of the leaf, $c = \sqrt{\frac{a^2(2a - 27\sqrt{2}}{-3(2a + 9\sqrt{2}}}$ and $c = \sqrt{\frac{b^2(2b - 27\sqrt{2}}{-3(2b + 9\sqrt{2}}}$ .

These three equations solve to $a = \frac{54 \sqrt{2} - 27}{7}$ , $b = \frac{54 \sqrt{2} + 27}{7}$ , and $c = \frac{27}{7}$ for $a < b$ , which makes the side length of the square $s = 2c = 2 \cdot \frac{27}{7} = \frac{54}{7}$ .

Therefore, $p = 54$ , $q = 7$ , and $p + q = \boxed{61}$ .