A Light Bulb Hanging From the Ceiling

Geometry Level 3

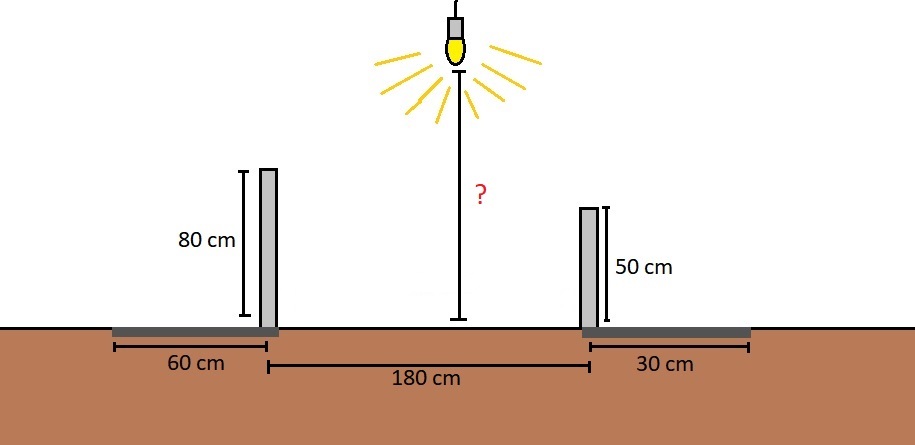
In the following image we have two poles with heights of 80 cm and 50 cm. They are 180 cm apart each other and we have a light bulb hanging from the ceiling between them. The post with height 80 cm casts a shadow of 60 cm on the ground. The post with 50 cm casts a shadow of 30 cm on the ground. How high the light bulb is hanging above the floor? (the diagram is not draw to scale)

150 cm 240 cm 90 cm 200 cm 180 cm

1 solution

Chew-Seong Cheong
Jul 20, 2018

Let the height of the light bulb above the floor be $h$ and the horizontal floor distance between the 80 cm post the light bulb be $a$ . Then by similar triangles, we have:

$\begin{cases} \dfrac h{60+a} = \dfrac {80}{60} & \implies 3h = 240+4a & ...(1) \\ \dfrac h{180-a+30} = \dfrac {50}{30} & \implies 3h = 1050-5a & ...(2) \end{cases}$

$(1) - (2): \quad 9a - 810 = 0 \implies a = 90$ . From $(1): \quad 3h = 240 + 4(90) \implies h = \boxed{200}$ .

A Light Bulb Hanging From the Ceiling

1 solution

0 pending reports