A limits problem

Calculus Level 3

find the limit (if possible):

Note:Use real numbers only.

$\lim_{x\to 0} \sqrt x$

1 0 Does not exist infinity

1 solution

Habib Mahdi
Jan 17, 2019

Algebraically: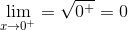

but:

Thus the limit does not exist.

By graph:

You can see that approaching 0 from the right = 0 , however, you can't approach 0 from the left. Therefore, the limit does not exist.

When $x<0$ , $\sqrt{x}=\sqrt{-x}i$ , so $\sqrt{-0}=\sqrt{0}i=0$ , the limit is 0.

X X - 2 years, 4 months ago

Sorry for not considering that in the question. But we are supposed to find the limit using real numbers only. You get a different solution if you use imaginary numbers. The domain of the square root function is the set of all non negative real numbers, however that's different if you include complex and imaginary numbers.

Habib Mahdi - 2 years, 4 months ago

A limits problem

1 solution

0 pending reports