A little bit of analytic geometry
Given a circle of radius 6 centered at the origin, and an ellipse of a semi-major axis of 5 and a semi-minor axis of 2 , you want to place the ellipse inside the circle such that its major axis is horizontal, and its center is below the origin, so that it is tangent to the circle at two symmetrical points about the vertical y -axis. If the right tangency point is ( x 1 , y 1 ) and the center of the ellipse is at ( 0 , y 0 ) , then find x 1 − y 1 − y 0 .
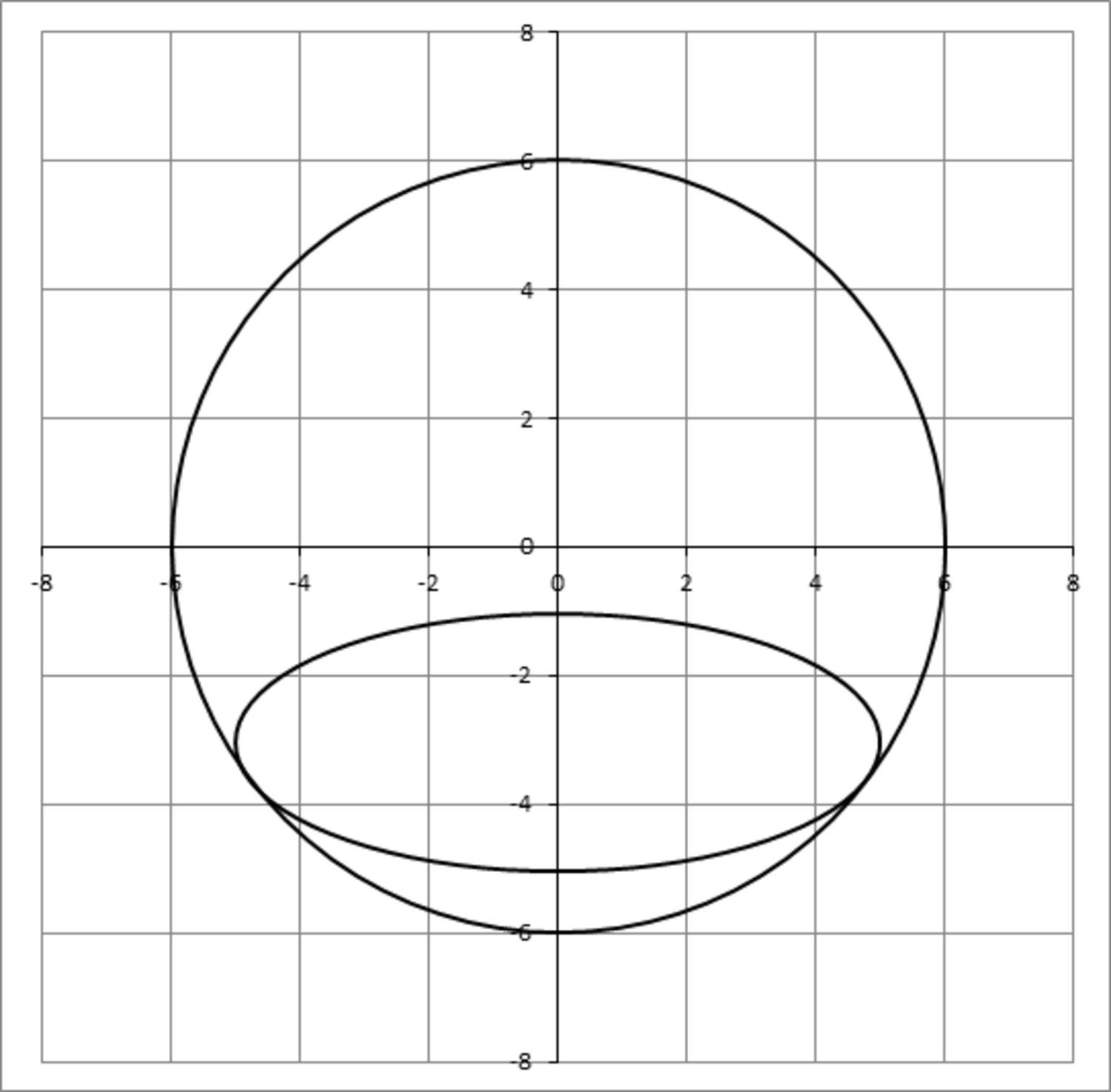
The answer is 11.444.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice alternative solution via calculus, Chew-Seong! Have a good day.....
Log in to reply
Thanks. I think it is easier and straight forward.
Let the ellipse have the equation 2 5 x 2 + 4 ( y − y 0 ) 2 = 1 and the circle be x 2 + y 2 = 3 6 . If we substitute x 2 = 3 6 − y 2 into the elliptical equation, we now obtain a quadratic in y :
2 5 3 6 − y 2 + 4 ( y − y 0 ) 2 = 1 ;
or 4 ( 3 6 − y 2 ) + 2 5 ( y − y 0 ) 2 = 1 0 0 ;
or 2 1 y 2 − 5 0 y 0 y + ( 2 5 y 0 2 + 4 4 ) = 0 ;
or y = 4 2 5 0 y 0 ± 2 5 0 0 y 0 2 − 4 ( 2 1 ) ( 2 5 y 0 2 + 4 4 ) = 4 2 5 0 y 0 ± 4 0 0 y 0 2 − 3 6 9 6 .
If the ellipse is to intersect the circle in only one value for y , then the discriminant above shall equal zero ⇒ y 0 2 = 4 0 0 3 6 9 6 ⇒ y 0 = ± 3 . 0 4 (of which we only admit the negative root as the ellipse lies entirely below the x − axis). This in turn yields the right-tangency point y 1 = 4 2 5 0 ( − 3 . 0 4 ) = − 3 . 6 1 9 , x 1 = 3 6 − 3 . 6 1 9 2 = 4 . 7 8 6 . The final desired result computes to:
x 1 − y 1 − y 0 = 4 . 7 8 6 − ( − 3 . 6 1 9 ) − ( − 3 . 0 4 ) = 1 1 . 4 4 5 .
The equations of the circle and the ellipse are
⎩ ⎨ ⎧ x 2 + y 2 = 3 6 2 5 x 2 + 4 ( y − y 0 ) 2 = 1 . . . ( 1 ) . . . ( 2 )
At the tangent point P ( x 1 , y 1 ) the gradients of the ellipse and the circle are the same. From differentiation with respect to x , we have:
⎩ ⎪ ⎨ ⎪ ⎧ ( 1 ) : 2 x + 2 y ⋅ d x d y = 0 ( 2 ) : 2 5 2 x + 4 2 ( y − y 0 ) ⋅ d x d y = 0 ⟹ d x d y = − y x ⟹ d x d y = − 2 5 ( y − y 0 ) 4 x
⟹ y 1 x 1 = 2 5 ( y 1 − y 0 ) 4 x 1 ⟹ y 1 = 2 1 2 5 y 0
From ( 1 ) − 2 5 × ( 2 ) :
y 1 2 − 4 2 5 ( y 1 − y 0 ) 2 2 1 2 2 5 2 y 0 2 − 4 2 5 ( 2 1 4 y 0 ) 2 2 1 2 5 y 0 2 ⟹ y 0 y 1 ( 1 ) : x 1 ⟹ x 1 − y 1 − y 0 = 3 6 − 2 5 = 1 1 = 1 1 = − 5 2 3 1 = 2 1 2 5 y 0 = − 5 2 1 1 1 = 3 6 − y 1 2 = 2 1 4 8 1 = 2 1 4 8 1 + 5 2 1 1 1 + 5 2 3 1 ≈ 1 1 . 4 Since y 0 < 0