A little twist on Irodov (Spring-pulley mechanics)
This is going to have a similar layout as problem 1.140 from Irodov. Consider the system below:
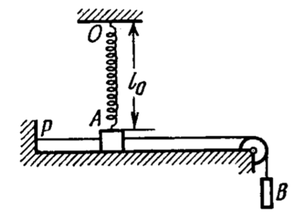
The origin of the system is at point . A bar rests on a horizontal plane and is connected to two weightless threads and, by means of a pulley, attached to a weight of the same mass as the bar. There is friction between bar and the plane it is on.
In addition, bar is connected to a spring hinged at point . At time , thread is burned, leaving the system to move. However, when the tension of the pulley thread exceeds of force, the pulley thread breaks and weight falls off, leaving no weight to pull on the bar.
Find the final stopping position of the bar, ie. the offset of the bar from the origin as declared above.
Relevant information:
- The mass of bar and weight is
- The natural length of the spring
- The spring constant
- Gravitational acceleration
- Coefficient of friction
The answer is 1.1116.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The original problem asks for the velocity of bar A when it breaks off the plane. However, an energy conservation approach can't be used since there's friction as well as the tension, which has to be computed.
The two equations of motion that can be found using Newton's 2nd law.
The normal force acting on bar A can be given by:
N = m g − F s sin ( θ )
The equation of motion for the movement of bar A is:
m x ¨ = T ± μ N + F s cos ( θ )
Since tension is acting opposite to gravity, the equation of motion for weight B is:
m x ¨ = m g − T
Rearranging the equation above for T and substituting into the equation on top, we can find an equation for the acceleration:
x ¨ = 2 m m g ± μ N + F s cos ( θ )
The code for the simulation is given below: