A little weirder!
If x + x 1 = 3 , find the value of x 1 5 + x 1 5 1 = ? .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
I think this is the best solution..
Log in to reply
indeed - very simple and elegant
Directly find roots of quadratic equation in terms of cube root of unity, put in equation. The simplest way. See my solution
I follow everything but am a little puzzled by the last line in your solution. Sorry, I'm not a mathematician so I can't easily write equations, but why in the line that starts "Then" do you have a minus sign in front of the parentheses that contain minus one over x to the 3rd power with a power of 5 outside the parentheses? If x to the 3rd is minus one over x to the 3rd, why are you suddenly minusing minus one over x to the 3rd? Doesn't that make that term equal to positive one over x to the 15th power and therefore the answer would be 2 over x to the 15th power instead of 0? Maybe it was just a typo or maybe I'm missing something. Hopefully this is clear!
Log in to reply
Sorry, my bad!! Yeah, This was typing mistake!! Thank you!! :)
You know what I some what used this logic only to solve the problem as I didn't know the identity (x + y)^5.
Anyways , it's a good solution. Keep it up!!
What the heck? You end up with a 1/0 . That's undefined. 0 can't be the answer
Log in to reply
Sorry that I don't get what you're trying to say! Would you please clarify your statement, please?
They're not asking for the value of x. They're asking for x to the 15th plus one over x to the 15th. Two different things.
x + x 1 ⇒ ( x + x 1 ) 3 x 3 + 3 x + x 3 + x 3 1 x 3 + 3 3 + x 3 1 x 3 + x 3 1 = 3 = ( 3 ) 3 = 3 3 = 3 3 = 0
And:
( x 3 + x 3 1 ) 3 x 9 + 3 x 3 + x 3 3 + x 9 1 x 9 + 3 ( 0 ) + x 9 1 ⇒ x 9 + x 9 1 = 0 = 0 = 0 = 0
Similarly,
( x 3 + x 3 1 ) 5 x 1 5 + 5 x 9 + 1 0 x 3 + x 3 1 0 + x 9 5 + x 1 5 1 x 1 5 + x 1 5 1 + 5 ( x 9 + x 9 1 ) + 1 0 ( x 3 + x 3 1 ) x 1 5 + x 1 5 1 + 5 ( 0 ) + 1 0 ( 0 ) ⇒ x 1 5 + x 1 5 1 = 0 = 0 = 0 = 0 = 0
I should have done this way.It was a lot simpler.Instead I made a quadratic equation and used quadratic formula to get the value of x(which was a complex number).Then I converted it into Polar Form and used DeMoivre's Theorem to raise it to 15th power. I got the answer as i.Then I substituted it back to get the answer as 0.
Log in to reply
It is okay. It is good that you have learnt.
that is the way i did it as well...a long way for a simple answer...
Let x = cos ( θ ) + i sin ( θ ) . Then x + x 1 = 2 cos ( θ ) = 3 . Take θ = 6 π . Now x 1 5 = cos ( 1 5 θ ) + i sin ( 1 5 θ ) = 0 + i . Then x 1 5 + x 1 5 1 = 2 cos ( 1 5 θ ) = 0 .
By far the simplest method.
Mind blowing
I used De Moivres Formula here.. Solving for the positive root we get, sqrt3/2 +(1/2)(i) then used The formula for the 15th power
We get the solution as i w , i w 2 put in the equation, use w 3 = 1 as w is cube root of unity, i 3 = − i to get result as 0 .
Assuming that f ( n ) = x n + y n , so we have: 1 . f ( 1 ) = 3 . 2 . f ( 2 ) = 1 . 3 . f ( n + 1 ) = 3 f ( n ) − f ( n − 1 ) . By resolving this we can see that f ( n + 6 ) = f ( n ) with every n > = 3 , so f ( 1 5 ) = f ( 3 ) = 0 .
( x + x 1 ) = 3
( x + x 1 ) 3 = x 3 + 3 ( x + x 1 ) + x 3 1 x 3 + x 3 1 = x 3 + x 3 1 − 3 ( x + x 1 ) = 3 3 − 3 3 = 0
It can also be observed that x 1 5 + x 1 5 1 = ( x 3 + x 3 1 ) ( x 1 2 + x 1 2 1 ) − ( x 9 + x 9 1 )
( x 3 + x 3 1 ) ( x 1 2 + x 1 2 1 ) = 0 ∵ ( x 3 + x 3 1 ) = 0
( x 3 + x 3 1 ) 3 = x 9 + x 9 1 + 3 ( x 3 + x 3 1 ) x 9 + x 9 1 = 3 3 − 3 3 = 0
Thus
x 1 5 + x 1 5 1 = 0 − 0 = 0
Plus it can also be generalised that when
x 3 + x 3 1 = 3
x y + x y 1 = 0 y = 3 n
when n is element of integer and n = 0
Moderator note:
Good observation about x 3 + x 3 1 and x 9 + x 9 1 .
In fact, your claim at the end can be strengthened. We have x m + x m 1 = 0 for numbers of the form m = 3 n , and not just those of the form m = 3 n .
Clearly, x = 0 . Multiplying both sides by x then using quadratics equation on x 2 − 3 x + 1 = 0 , we have x = 2 3 ± i = c i s ( ± 6 π ) .
It doesn't matter which root we use for x because r 1 1 5 = r 2 1 5 1 if we let those two roots be r 1 and r 2 . So WLOG, let x = c i s ( 6 π ) . Then x 1 5 + x 1 5 1 = c i s ( 6 1 5 π ) + c i s ( − 6 1 5 π ) = 2 cos ( 2 5 π ) = 0 .
I have another easy solution.
Then,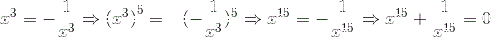
That's the solution!!