A logic problem by Chandrakant Pandey
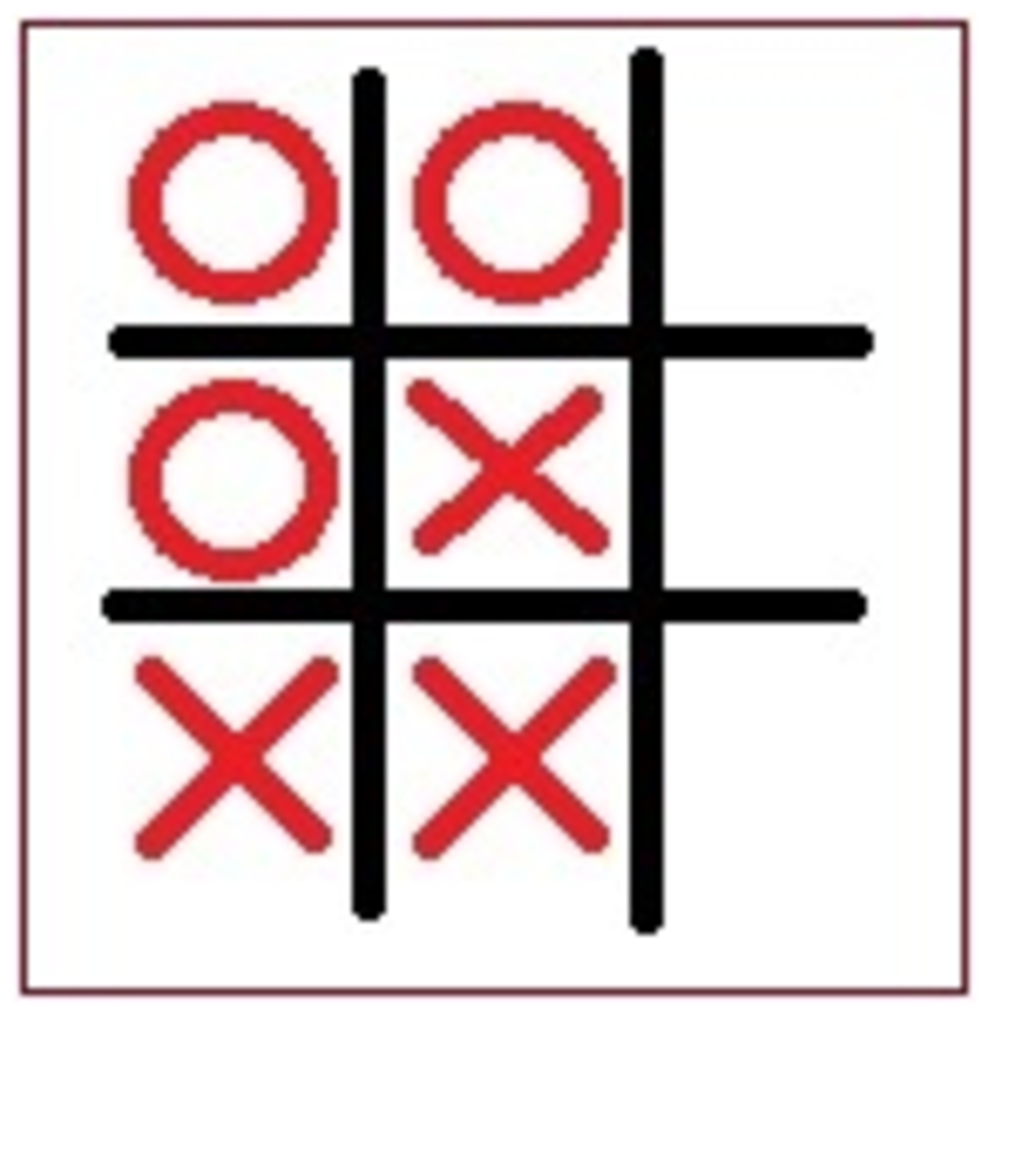
Ank and Mini play a game of tic-tac-toe. where they try to get three circles or three crosses in a row (horizontal, vertical, or diagonal).
They are both rational players, hence obey the following rules in order:
- Immediate win: If a player can place his own symbol in a row that already contains two of this own symbols, then he will do so.
- Avoid immediate loss: If a player can place his own symbol in a row that already contains two of his opponents symbols, then he will do so.
- Do anything else: There is no prescribed strategy other than that listed above.
In the above game, six moves have been made. Ank plays with crosses (X) and Mini plays with circles (0). However, we do not know who started the game. Who will win the game?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the next player to play will win the game by placing his symbol in the top right corner, the crucial crux of this problem is figuring out whose turn is next. We do so by analyzing the steps that lead up to this current state. Label the board as follows on the right. We will refer to the squares by the numbers on them.
Observe that 2 , 5 , 4 , 8 , 1 , 7 is a valid sequence of moves that obeys the given rules and leads to this final state. If X indeed played the 6th step, then this tells us that O plays the 7th step and hence wins.
We prove by contradiction that X has to play the 6th step.
Suppose not. If O plays the 6th step, then X has marked out 5 , 7 , 8 . Since 3 was not played, this means that O must have "Avoided immediate loss" by playing at 2.
Then, X at the 5th step is facing 1 , 4 played by O:
If X previously played 5 , 7 , he could immediately win by playing 3 .
If X previously played 7 , 8 , he could immediately win by playing 9 . If X previously played 5 , 8 , he could immediately win by playing 2 (Rememeber that 2 was only claimed in the 6th step, so is free to X in the 5th step) .
This tells us that X under the scenario of O playing the 6th step, X could have won at the 5th step. Hence, O did not play the 6th step, so X played the 6th step.
Since 254817 a valid gameplay, we can now conclude that O has to play the 7th step and hence win the game.
Note: There are several valid gameplays, like 254817, 284517, 452817, 482517.
Before reading further, can you prove that 1) the 6th step must be 7 and 2) the 5th step must be 1?
Since X plays the 6th step, then O has previously marked out 1 , 2 , 4 . Since 3 was not played, this means that X must have "Avoided immediate loss" by playing at 7.
Then, O at the 5th step is facing 5 , 8 played by X.
If O previously played 1 , 2 , he could immediately win by playing 3.
If O previously played 1 , 4 , he could immediately win by playing 7 (Remember that 7 was only claimed in the 6th step).
Hence, we conclude that O previously played 2 , 4 , and his 5th step was to play 1 .