A logic problem by Chung Kevin

In an equation, we have:

$\begin{aligned} (20+W)W & = 120 + W \\ W^2 + 20W & = 120 + W \\ W^2 + 19W -120 & = 0 \\ (W-5)(W+24) & = 0 \\ W & = \boxed{5} & \small \color{#3D99F6} \text{Since } W \ge 0 \end{aligned}$

$W \times W$ results in a product with last digit $W$ . The only numbers whose square $W^2$ results in a product with the last digit being itself $W$ are:

$0 \ : {\color{#EC7300}{0}} \times {\color{#EC7300}{0}} = {\color{#EC7300}{0}}$

$1 \ : {\color{#D61F06}{1}} \times {\color{#D61F06}{1}} = {\color{#D61F06}{1}}$

$5 \ : {\color{#3D99F6}{5}} \times {\color{#3D99F6}{5}} = 2{\color{#3D99F6}{5}}$

$6 \ : {\color{#20A900}{6}} \times {\color{#20A900}{6}} = 3{\color{#20A900}{6}}$

Our product is nonzero, so $W \neq 0$ .

Because our product is in the hundreds, $W \neq 1$ .

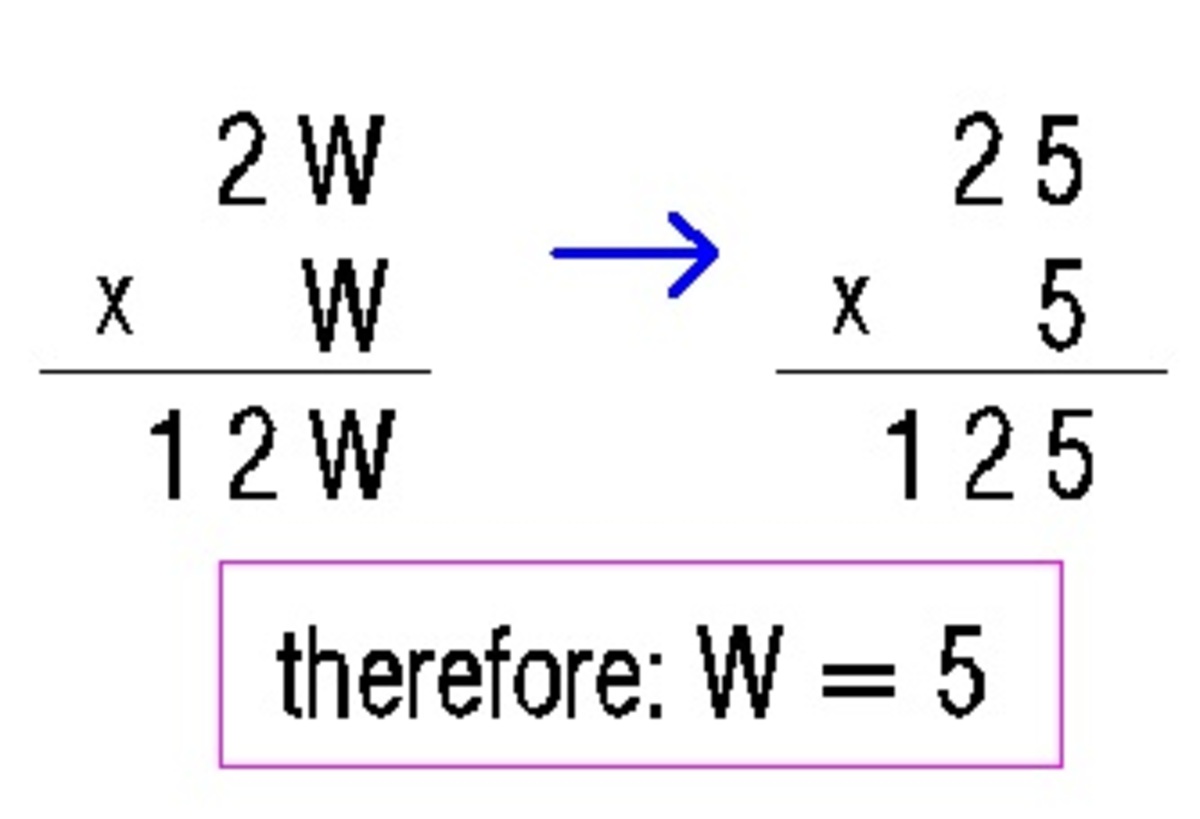
Testing $5$ and $6$ , we get that $W = 5 \ :$

$2{\color{#3D99F6}{5}} \times {\color{#3D99F6}{5}} = 12{\color{#3D99F6}{5}}$

$\begin{array} { l l l l l } & & 2 & 5\\ \times & & & 5\\ \hline & 1 & 2 & 5\\ \end{array}$

Firstly, we have to find numbers that when squared, give the same number in the unit's place as the original number. So the number could only be either 0,1,5 or 6. Now, we just use trial and error to triy 0,1,5 and 6. At last, you would find that the answer is 5

here,
$(20+w)*w=120+w$
or, $w^2$ +19w-120=0 or, $w^2$ +24w-5w-120=0 or, (w+24) (w-5)=0 so w=5 where w>0 ans#5