Pitiless Rooks
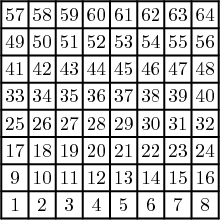
A chessboard is numbered as the figure shows. rooks are placed such that any rook can capture at least another rook. The numbers where the rooks were placed are added up. Considering all the possible accommodations, how many distinct sums can be obtained?
Inspiration .
The answer is 449.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
All possible number of sums that can be obtained from any 8 values of the squares can be obtained from configurations of 8 rooks that respect the conditions of the problem that is a number of 449 sums anyway.
To count all possible sums that can be obtained from good configurations of rooks (a "good" configuration respects the conditions of the problem) the approach would be to start from the smallest possible sum and it's corresponding configuration meaning the configuration made from the rooks which stand (on the squares with smallest possible values) on the first row and observe how many sums can be generated by changing the smallest possible number of rooks of the initial configuration until the sum corresponding to all rooks standing in the next row , and from that one to the next and so on.
By starting from an initial sum corresponding to a configuration of 8 rooks in only one row it should be understood how to provoke an increase for that initial sum such that all possible values until the sum which corresponds to all 8 rooks standing in the next row are obtained which would imply understanding the way in which the sum and the increase can be obtained by changing rooks from the starting configuration. Because exactly this change of rooks provokes an increase , therefore it is dependent just on it , the understanding of this way or relation which speaks about how the sum is increasing by the change of positions of rooks has to be considered as sufficient in determining the possibility of sums which can be thought abstractly. Therefore what will be done from here is to consider exactly this possibility , thought a priori as possibility in conceiving it of sums abstractly. This meaning an abstract understanding regarding what conditions anyway the possibility , thought as abstract possibility , of generating sums so to say.
Name the rows from the one with the smallest sum of values of squares to the one with the biggest values R1 , R2 and so on. To obtain an abstract understanding of the way by which an initial sum can be increased by changing positions of some rooks from the 8 rooks which are standing in the same row consider precisely this change by organizing it around understanding the cumulative law of how to obtain the consecutive increases which generate all the sums possible by changing the least number of rooks anyway. For changing the position of 1 rook from an initial configuration 8 rooks standing in a row that rook should be move any number of squares from it's initial place different from 8 or a multiple of 8 (since if it moves a number multiple of 8 it will be on the square immediately above the initial place and not attack rooks) by this meaning that all possible increases that it can generate to the initial sum will contain all numbers until the initial sum (S1) and the last square on which it can stand (square 64) therefore generating all sums between S1 and S1+ (64-q) for q being the initial square of the rook without multiples of 8. To obtain all values that are until 64-q therefore the multiples of 8 there will be necessary at least 2 rooks anyway and to also show this is possible consider taking 2 consecutive rooks from the last half of the row and place them after a number of 8k/2 each squares where k * 8 is the multiple of 8 which because they are consecutive and are increasing at a rate of 8/2=4 will repeat 2 times in the same places giving always good configurations.
Therefore for any row for changing at most 2 rooks all possible sums between Si and Si+ 64-q can anyway be obtained , where q can be thought from now on as the smallest possible value of the row anyway.
Now , observe that for some rows, for choosing q as the smallest possible value of the row this value isn't anyway covering all possible sums requiring for those sums a change of more than 2 rooks. Because considering the rows their qs are increasing with 8 the number of possible increases (that being the number 64-q) using just 2 rooks with will decrease with 8 , 8*2 and the relation being inverse proportionally anyway considering the increase in the rows.
It is also important to note that if until the half of the rows by this procedure can be obtained all anyway possible sums between consecutive rows then also all possible sums between the second half anyway. Considering the other half , what has to be done is to take rooks a place them in a decreasing order therefore not in the front of the rows but before them to make the sum lesser anyway.
Next , it would be better to express the relation of increase between the number of increases that anyway can obtained using more than 2 rooks and the number of increases necessary for the increasing rows.
The second relation has been established being saw that as the number of rows increases the number required sums which use more that 2 rooks gets bigger anyway with m * 8 , (m+1) * 8 and so on anyway.
For taking 2 rooks observe that there can be obtained as for taking 1 rook all increases from 63-q1 but excepting those increases which are multiples of 8 and which are of the form 8k+1. In a similar way anyway for taking 3 rooks there can be obtained all increases from 62-q2 excepting all the 8 , 8k+1 , 8k+2 and for taking 4 rooks all increases excepting those of the form 8 , 8k+1 ,8k+2 ,8k+3 until 61-q3 and so on helping for deriving a general formula for this. To prove therefore that for taking n rooks all increases possible anyway can be obtained in the condition of the problem it should be proved that for all numbers until the one of the form 8k+n-1 there is a way to obtain also those numbers by changing rooks which can be done by considering things generally too anyway. Because however , all the sums necessary to prove here anyway are just until the row 4 and therefore 24 sums it is sufficient to prove that 2 rooks changed are enough because they cover the necessary increase just thinking in the concrete terms of changing rooks and not proving abstractly for any number of rooks changed from a row.
Therefore for taking 2 rooks starting from the sum obtained at 64-q and therefore having a rook in anyway the final row at 64 firstly observe that all numbers of 8k+1 can be obtained. For that it is necessary to decrease the value of the rook at the square 64 and increase the value of another rook from the initial configuration anyway of rooks such that the increase is regulated on the right amount to obtain for any of the 3 rows considered all the other possible cases. Obtaining also the multiples of 8 of course as increases it anyway can be said is necessary that there will be taken 2 rooks from the configuration of the rooks on the row. Forwardly and fast this can be done also as for 1 rook , taking consecutive rooks which will stand and therefore have the same characteristics stated earlier.
By this finally this proof , though it can be considered generally and faster as shown can be anyway considered done so to say anyway.
It is also interesting to note that all possible arrangements for obtaining the sums maybe can be expressed in another form of organization which leads to some other not completely abstract proof anyway.