Win a Car Game Show

Probability Level 1

You are in a game show. The purpose of the game show to correctly guess behind which of three doors lies a fancy car - your prize if you win. Behind the other two doors lie some goats. The game show host first asks you to guess one door, then - without showing you what lies behind your door - shows you another door with a goat behind it. He then asks whether you want to switch your guess from your original door to the other remaining door. Should you switch, and what is the maximum probability that you would win the car?

yes, 1/2 no, 1/2 yes, 2/3 no, 1/3

Meilong Zhang by Meilong Zhang , 20, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Harsh Khatri
Feb 14, 2016

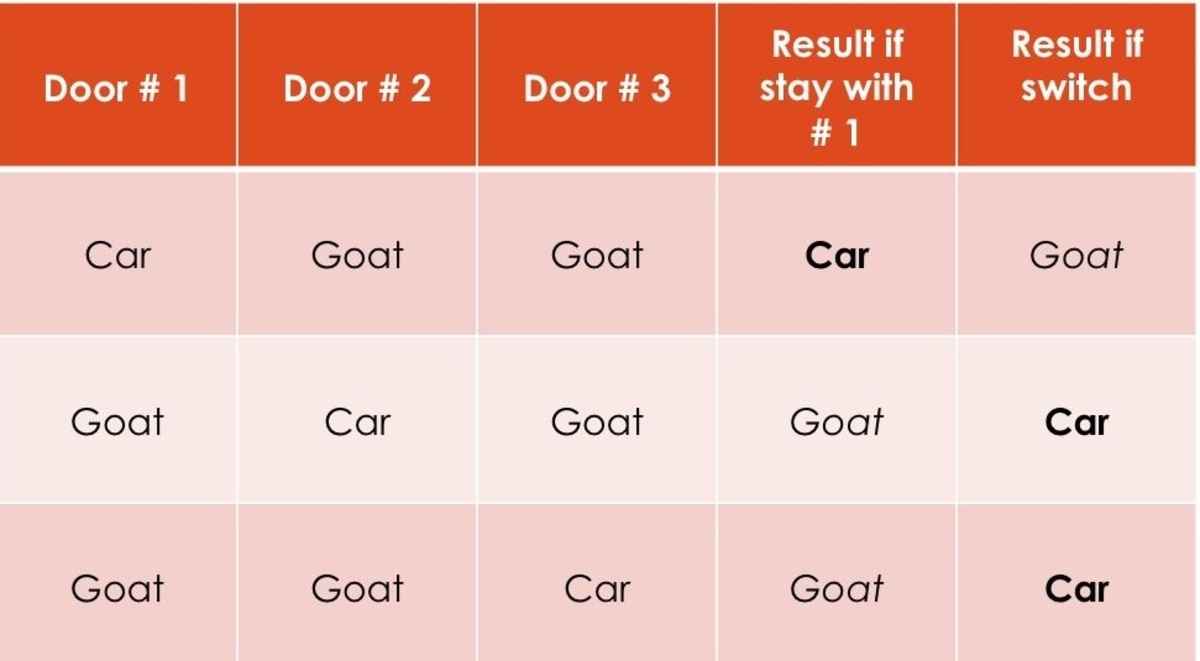
One can win in two ways:

(A) Select the correct door in the first guess itself.

(B) Select the wrong door in the first guess and then switch after the host shows the goat behind one of the doors.

⇒ P ( w i n ) = P ( A ) + P ( B ) \displaystyle \Rightarrow P(win) = P(A) + P(B)

⇒ P ( w i n ) = 1 3 + 2 3 × P ( s w i t c h ) \displaystyle \Rightarrow P(win) = \frac{1}{3} + \frac{2}{3} \times P(switch)

⇒ P ( w i n ) = 1 3 + 2 3 × 1 2 \displaystyle \Rightarrow P(win)= \frac{1}{3} + \frac{2}{3} \times \frac{1}{2}

⇒ P ( w i n ) = 1 3 + 1 3 \displaystyle \Rightarrow P(win) = \frac{1}{3} + \frac{1}{3}

⇒ P ( w i n ) = 2 3 \displaystyle \Rightarrow P(win) = \boxed{\frac{2}{3}}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Nicely done!

Meilong Zhang - 5 years, 4 months ago

Log in to reply

Thank you!!

Harsh Khatri - 5 years, 4 months ago
Meilong Zhang
Feb 14, 2016

If you were to begin by choosing an incorrect door, then by switching you would have a 2/3 probability, since there are 2 incorrect doors and only 1 correct door.

Think about it this way:

From this we can see that if you don't switch, you would only have a 1/3 chance of winning because there was only one correct door in the first place. However, if you switch, you are swapping the two, so the 2 incorrect doors would become correct and the one correct would become incorrect. So, the answer is you should switch, and the probability is 2/3 for winning.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...