A Lot of Methods

Since $\angle AFB = \angle ADB$ , this implies $AFDB$ is cyclic which implies that $\angle ABF = \angle ADE$ which implies that $\triangle ABF \equiv \angle ADE$ . This implies that $\frac{AD}{AB} = \frac{AE}{AF}$ which implies that $FE = 4 \implies DF = \frac{16}{5}$ .

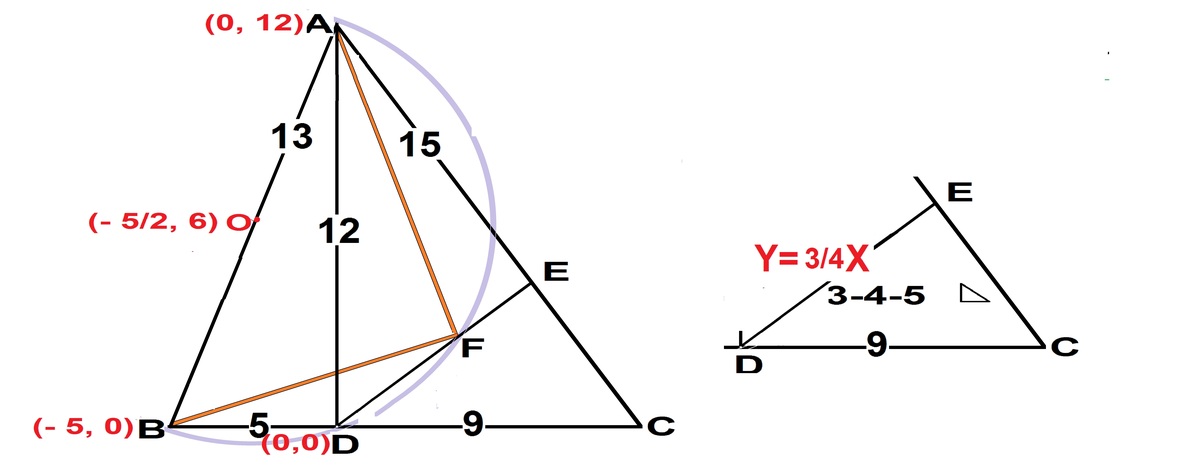
$\Delta~ABC~ is ~ made ~ up ~ of ~ two ~ rt. ~ \angle ed ~ \Delta s~ ADB ~and ~ ADC,~ where~~AD=5, ~ and ~ DC=9, ~ and ~ AD=12.\\ Since ~ AB ~ is ~ the~ hypotenuse~ of ~ two~ rt~ \angle ed ~ \Delta s ~ \text{ADB and AFB, it is the diameter of a circle.}\\ \text{O, the midpoint of AB is the center and radius }=\dfrac{13} 2.\\ \text{DE is the altitude of the 3-4-5 rt } \angle e~ \Delta ~ ADC. ~ So ~ TanEDC = \dfrac 3 4 .\\ \text{Let A(0,12), B(- 5,0), D(0,0) be ~ on ~ x-y plain.}~\therefore~0(-\dfrac 5 2, 6).~~F = the~ circle\cap DE.\\ \implies~(X+\dfrac 5 2 )^2+(Y- 6)^2=\left \{\dfrac{13} 2 \right \}^2\cap Y=\dfrac 3 4 X. ~ Solving, ~ we ~ get ~ F(0,0) ~ 0R ~ F\left (\dfrac{64}{25}, \dfrac{48}{25}\right ).\\ Since D(0,0), ~ F\left (\dfrac{64}{25}, \dfrac{48}{25}\right ).~ \therefore DF=\dfrac{16}5=\dfrac m n.~~~So~~m+n=\large~~~~~~~~~~\color{#D61F06}{21}$