Crowded Pawns

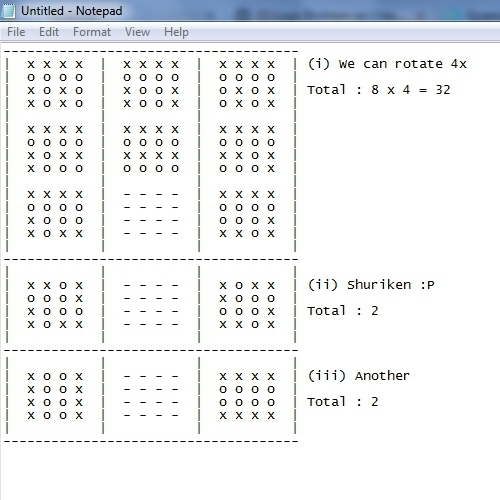
First take note that putting a pawn on a colored tile (black or white) meant that on all four tiles directly diagonal to it you are not allowed to put another pawn (as they attack or be attacked by the first pawn). However, this first pawn doesn't affect the pawns in other tiles other than these 4 diagonal tiles - hence positions of pawns in white tiles are independent of positions of pawns in black tiles.

Then, we need to find to find the maximum number of pawns to fit into tiles of one color (e.g. black). Due to small board size, it is possible to manually determine that at most 4 black tiles have pawns, and that there are 6 configurations to allow this. Likewise there are also 6 configurations of most pawn pieces in white tiles due to symmetry.

Total configuration of all pawns = 6 $\times$ 6 = $\boxed{36}$

Firstly organize the chessboard by considering the set of all black squares on the chessboard and the set of all white squares on it separately. A pawn put in a square of a color will attack only squares of the same the color which are in the front of the pawn. The configuration of pawns and all the squares which are therefore attacked by them which are of interest in calculating the maximum number of pawns that can be put to respect the conditions of the problem can be then thought generally as made from the configuration of all pawns placed on white squares and of all pawns placed on black squares. To calculate the maximum number of pawns abstractly observe that every row (or column) has 2 squares of each color and also that if a pawn will be placed on a square it will eliminate the possibility of at least one square of the same color in an adjacent row implying the maximum distribution of pawns is for squares of a color , if possible , 2 * 2 = 4 pawns for one color and 4*2=8 for the entire chessboard.

Now, for understanding if any and which configurations works for 8 pawns and therefore find the number of configurations that work which is required by the problem one approach this is to consider things constructively. That implies understanding the concrete way the placing of the pawns on the chessboard affect placing other pawns which therefore implies arriving at an understanding of how for a configuration of pawns will correspond the set of attacked squares and therefore asks for an understanding which , by a constructive approach , is or seems pretty difficult to formulate well enough in abstract terms. One way for achieving an understanding of this is to divide the chessboard in 4 smaller 2X2 squares where in each of the squares you can put at most 2 pawns on squares of different colors and therefore in order to achieve the maximum number of pawns as there are 4 such squares it is necessary to put 2 pawns in all 4 2X2 squares. To understand further the way in which placing the pawns affects the general configuration , thinking in the terms of this 2X2 squares , it can be said that for some configuration of pawns chosen in one 2X2 square it will affect the possible configurations in some of the other 2X2 squares and therefore what is to be followed is how this concrete way of affecting the squares happens. Now , any of the 2 pawns can be put in the 2X2 squares either in the corner of the chessboard or in one of the squares from the center of the 4X4 chessboard and observe that for the way it is chosen to place them the way it affects the possible positions of the pawns in the other 2X2 squares will be different. Note that for placing a pawn in one of the squares of some color in the center of the 4X4 chessboard it will affect one square of 2 of that same color of all the other 2X2 squares remaining which implies that all those 2X2 squares will remain with just one possibility to place pawns in one of the squares of that color and therefore that for a pawn in a central square there is only one configuration possible. Therefore all possible configurations can be taught by the way the pawns are placed in all the 2X2 squares , and counted in the terms of placing pawns in center of the chessboard. There are 3 possibilities : either to put 2 pawns in the center , to put just 1 in the center and to not put any. For placing 2 pawns in the center of the chessboard since they have to be of different colors and are 2 squares of each color in the center there is a number of 4 configurations to choose them which will all have 1 possible configuration , therefore for placing 2 pawns in the center will be 4 * 1 = 4 possible configurations. For placing 1 there are 4 ways to place the pawns in the center and for any of them in the remaining 3 2X2 squares the position of the pawns of the 2 2X2 squares which have a square of a different color that the one chosen for the pawn in the center will be decided and therefore will be just 1 configuration and for the remaining 2 2X2 squares will be , as a pawn can be put in 2 places without affecting the positions of the other , 2 possible configurations as such 2 *2 ways to place the pawns in the remaining 2 squares of 2X2 therefore 4 * 2 * 2=16 possible configurations for a pawn in the center. Finally for placing 0 pawns in the center then all 4 2X2 squares behave in the same way as in the second case because one position for a pawn is already decided (namely for all 2X2 squares will pawns in the corner) remaining a number of 2 possible cases to choose for each 2X2 square that will not affect the possibilities of the other squares being therefore for each of the 4 2 possibilities and as such 2^4=16 possible configurations. This means that the total number of configurations possible regarding the center is of 4 + 16 + 16 = 36 configurations which is therefore the answer to the problem. This way anyways , is maybe not the best to understand how the pawns affect each other as it is not the most abstract. Also more interesting would be to consider things for any nxn chessboard generally anyways.