A Lot Of Rooks!
Probability
Level
2
Dimitri places the maximum possible number of Rooks on a chessboard in such a way that there's no two Rooks that attack each other. In how many ways can he do that?
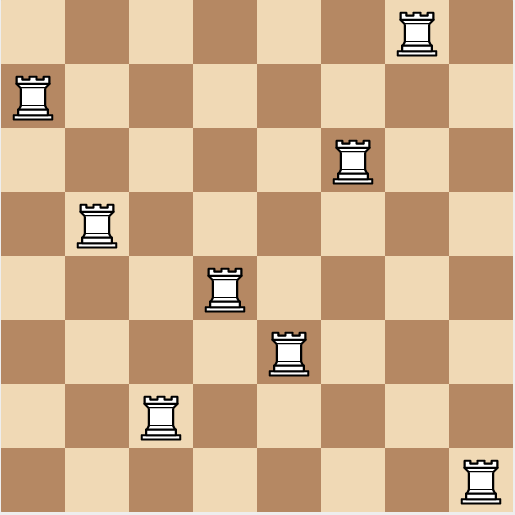
The answer is 40320.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Permutations - Problem Solving
He can place at most 1 rook in each column and row, because if he places 2 or more, they will be attacking eah other. As each row consists of 8 squares, he has 8 possible squares to place the first rook. In the next row, there will be only 7 squares available as one square will be under attack by the first rook. Continuing with this reasoning, for the eighth rook, there is only one square available. Therefore, the answer is simply 8 ! = 4 0 3 2 0 .