A lot of tangency points

Geometry Level 4

The triangle $ABC$ is inscribed in the circle $\mathcal{C}$ . Circle $\mathcal{C}_1$ is tangent to the minor arc $AB$ of $\mathcal{C}$ and to side $AC$ at point $P$ . Circle $\mathcal{C}_2$ is tangent to the minor arc $CB$ of $\mathcal{C}$ and to side $AC$ at point $Q$ . From point $B$ draw the tangents $BR$ and $BS$ to circles $\mathcal{C}_1$ and $\mathcal{C}_2$ , respectively. It is known that $BA=22$ , $BC=23$ , $BR=16$ , $BS=17$ , $PQ=15$ . $AC$ can be written as $\frac{a}{b}$ , where $a$ and $b$ are coprime positive integers. What is the value of $a+b$ ?

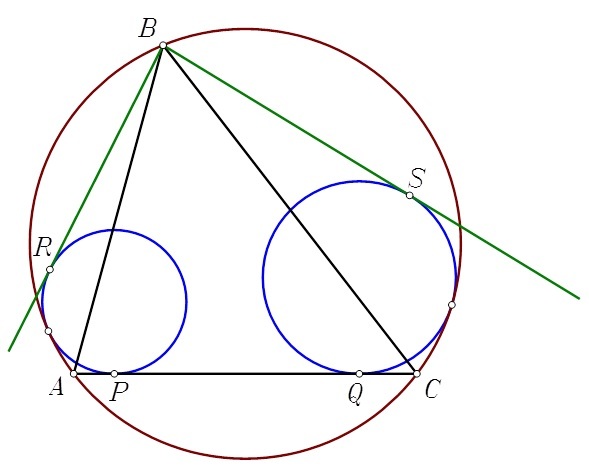
The answer is 236.

1 solution

Andrea Pozzoli
Dec 21, 2013

We use Casey' s theorem. We denote with T(a,b) the length of the tangency segment between A and B. First we consider the 4 circles C2, A (degenerate circle), C1 and B(degenerate circle). We have T(C2,A)xT(C1,B)+T(A,C1)xT(B,C2)=T(C2,C1)xT(A,B). So we have AQxBR+APxBS=PQxAB, which is equal to (AP+PQ)x16+APx17=15x22 ---> (AP+15)x16+APx17=15x22 --->33xAP=15x6 ---> AP=30/11. Then we consider the 4 circles C2, C (degenerate circle), C1 and B(degenerate circle). We have T(C2,C)xT(C1,B)+T(C,C1)xT(B,C2)=T(C2,C1)xT(C,B). So we have CQxBR+CPxBS=PQxCB, which is equal to CQx16+(CQ+QP)x17=15x23 ---> CQx16+(CQ+15)x17=15x23 --->33xCQ=15x6 ---> CQ=30/11. So we have AC=AP+PQ+CQ=225/11, so a+b=236. Sorry for the bad latex, but i didn't manage to format the text well.

" Sorry for the bad latex, but i didn't manage to format the text well."

Stefano Scx - 7 years, 5 months ago

LOL

Andrea Pozzoli - 7 years, 5 months ago

Are you sure that the circles $\mathcal{C_1}$ and $\mathcal{C_2}$ dont intersect with each other? Because if they intersect, then Casey's theorem is not valid.

Mridul Sachdeva - 7 years, 5 months ago

We could use Casey's theorem on $A, B, C$ and $C_1$ .Here we are sure that $A, B, C$ don't belong to $C_1$ . We obtain, calling $AP$ $x$ and $CQ$ $y$ : $BC \cdot AP+ (x+y+15)\cdot BR= AB \cdot (15+y) \to 23x+16x+16y+16\cdot 15 = 22 \cdot 15 +22y \to 39x-6y=90$ . Using Casey's theorem on $A, B, C$ and $C_2$ , we obtain $BS \cdot (x+y+15) + y \cdot AB= BC \cdot (x+15) \to 17x+17y+17\cdot 15 + 22y = 23x+23\cdot 15 \to 39y-6x=90$ . Solving the sistem we obtain the same results i have told before. Is that correct (thank you for the observations) ?

Andrea Pozzoli - 7 years, 5 months ago

Yeah.. Anyways they have drawn the figure now! :)

Mridul Sachdeva - 7 years, 5 months ago

A lot of tangency points

The answer is 236.

1 solution

0 pending reports