A lovely one
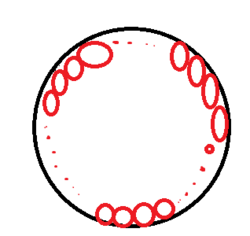If , inside a big circle , exacty 36 small circles , each of radius 5 , can be drawn in such a way that each small circle touches the big circle and also touches both its adjacent small circles , then the radius of the big circle is a
Find [ a ]
Clarification -
-
The image is just shown to understand the given situation , here all the small circles are of same radius and each one touches its adjacent one and the circle in which it is inscribed.
-
[.] - Greatest integer function
Note - If you can give a general formula for the radius of the big circle such the there are more than or equal to 3 small circles inscribed in it , you will be appreciated
The answer is 62.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
As for a general formula, with n adjacent circles each of radius r the radius R of the big circle is
R = 1 − cos ( n 3 6 0 ∘ ) 2 ∗ r + r .
Log in to reply
or the general formula can be written as R = r ( 1 + c o s e c n π )
Log in to reply
Yes, that's a much better expression.
1 − cos ( n 2 π ) = 2 ∗ sin 2 ( n π ) , transforming my formula to
R = 2 sin 2 ( n π ) 2 ∗ r + r = r ( 1 + csc ( n π ) )
as you have found.
THEGENERAL FORMULA FOR RADIUS OF BIG CIRCLE (R) TO ACCOMODATE n NO SMALL CIRCLE (RADIUS r ) IS R = r(1+Cosec pi/n) , for n greater than equal to 3.
Give a proof for that formula
Log in to reply
this question is an absolutely fantastic problem!!!the problem maker is a genius!!!thanks for posting this wonderful problem!
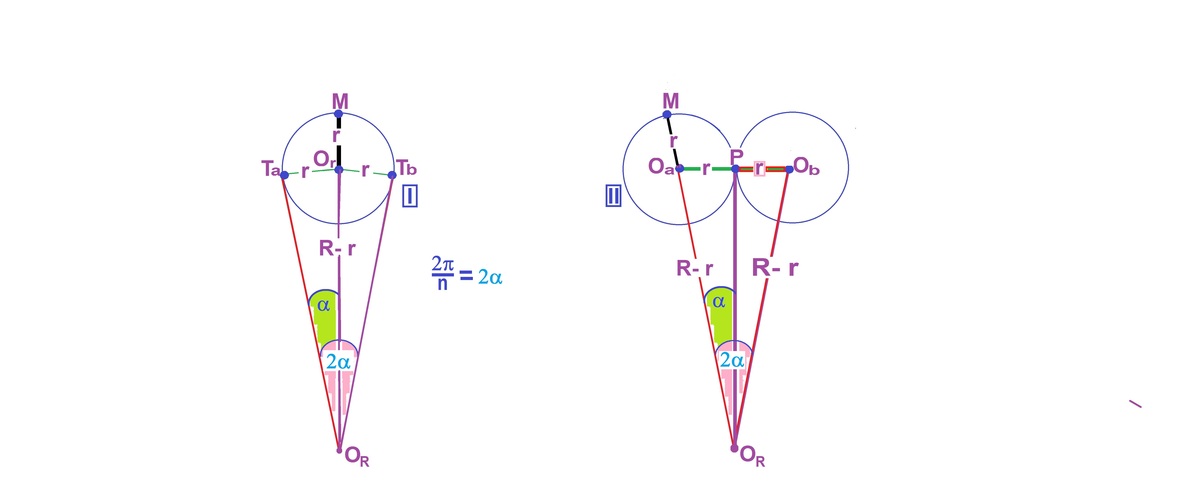
In response to Mark Vincent Mamigo, I am up loading two images and two ways of solving.
There are n circles of radius r ,[ with centers
O
r
,
O
a
,
O
b
,
shown ], in a big circle of radius R and center
O
R
as per condition in the problem.
M
i
s
t
h
e
p
o
i
n
t
o
f
t
a
n
g
e
n
c
y
w
i
t
h
t
h
e
b
i
g
c
i
r
c
l
e
.
I
n
[
I
]
,
T
h
e
a
n
g
l
e
b
e
t
w
e
e
n
t
w
o
t
a
n
g
e
n
t
s
O
R
T
a
a
n
d
O
R
T
b
=
n
2
π
=
s
a
y
2
α
.
O
R
T
b
O
r
T
a
f
o
r
m
a
c
y
c
l
i
c
k
i
t
e
r
i
g
h
t
a
n
g
l
e
a
t
p
o
i
n
t
s
o
f
t
a
n
g
e
n
c
y
T
a
,
T
b
.
I
n
t
h
e
r
i
g
h
t
△
T
a
O
R
O
r
,
∠
T
a
O
R
O
r
=
α
,
O
r
O
R
=
M
O
R
−
M
O
r
=
R
−
r
.
S
o
l
v
i
n
g
t
h
i
s
Δ
,
w
e
g
e
t
(
R
−
r
)
S
i
n
α
=
r
.
∴
R
=
r
∗
(
1
+
S
i
n
α
1
)
I
n
[
I
I
]
,
T
h
e
a
n
g
l
e
b
e
t
w
e
e
n
l
i
n
e
s
j
o
i
n
i
n
g
c
e
n
t
e
r
s
O
R
O
a
a
n
d
O
R
O
b
=
n
2
π
=
s
a
y
2
α
.
T
h
e
t
w
o
s
i
d
e
s
O
R
O
b
a
n
d
O
R
O
a
w
i
t
h
v
e
r
t
e
x
a
n
g
l
e
2
α
f
o
r
m
a
n
i
s
o
s
c
e
l
e
s
Δ
O
a
O
R
O
b
.
I
n
t
h
e
r
i
g
h
t
△
O
a
O
R
P
,
∠
O
a
O
R
P
=
α
,
O
a
O
R
=
M
O
R
−
M
O
r
=
R
−
r
.
S
o
l
v
i
n
g
t
h
i
s
Δ
,
w
e
g
e
t
(
R
−
r
)
S
i
n
α
=
r
.
∴
R
=
r
∗
(
1
+
S
i
n
α
1
)
α
=
2
3
6
3
6
0
=
5
o
.
R
=
5
∗
(
1
+
S
i
n
5
1
)
=
6
2
.
3
6
8
.
⌊
6
2
.
3
6
8
⌋
=
6
2
I don't know how to put a drawing.. Just imagine this: inside the big circle, there are 36 small circles with radius 5.. If we tend to imagine, connecting the radii will form a polygon with 72 sides.. Dividing one side of the polygon (which is the radius of the smaller circle) will yield 2.5 units.. We now have a right triangle.. The angle opposite the 2.5 units will be 360/72=2.5 degrees.. Getting the value of the hypotenuse, we have 2.5/sine (2.5 degrees)=57.31396407.. Adding 5 (the radius of the smaller circle) will yield the radius of the bigger circle which is 57.31396407+5=62.31396407 units.. Getting its G.I.F., we have 62..
I hope someone can upload an image to my solution for the benefit of everybody.. I really don't know how to upload an image for my solution..
I think it is 36-gon and not 72-gon. Since I can not up load an image directly here I am putting in my solution.
Let centre and radius of bigger circle be C and R respectively and centre of 2 consecutive small circles be O 1 and O 2 .
Join O C 1 C 2 .
Now, ∠ O 1 C O 2 = 3 6 3 6 0 = 1 0 ° O 1 O 2 = 1 0 , C O 1 = C O 2 = R − 5
Using cosine rule, one can get R easily which would be 62.368, so our answer will be 6 2