Trapezium With Quadrilateral
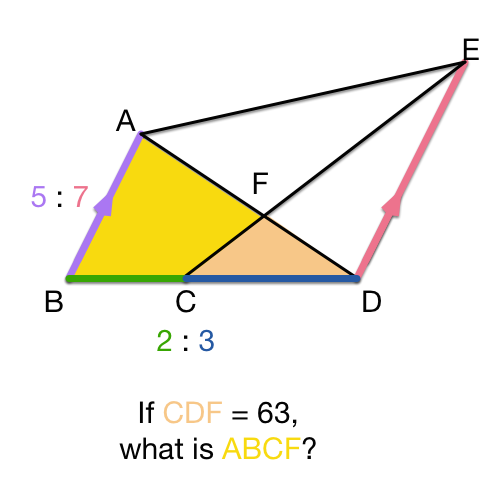
In the figure, , and are straight lines. It is given that is parallel to , and . If the area of is , then what is the area of ?
Source: Lingnan Secondary School Post-Mock Exam Paper.
Thanks to my student Chang Chi Kong for his contribution.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let X 1 , X 2 , ⋯ , X n be the points on an R 2 plane. In the following, we denote the area of an n -sided polygon X 1 X 2 ⋯ X n by ( X 1 X 2 ⋯ X n ) .
Solution
Let A B = 5 k , D E = 7 k , B C = 2 h and C D = 3 h for some positive constants h and k (as labelled in the figure).
In the figure, we construct a point G on A D such that joining C G yields the result C G // B A . Then we have C G // D E . Now, it is readily seen that
( 1 ) ( 2 ) △ C G F △ D A B ∼ △ E D F , and ∼ △ D G C .
For (2), the proportionality of the corresponding sides gives C G = 3 k ; and then, for (1), it gives G F : D F = C G : E D = 3 : 7 . Since △ C F G and △ C F D have the same height relative to their respective bases G F and D F , we have ( C G F ) = ( C D F ) ⋅ D F G F = 6 3 × 7 3 = 2 7 cm 2 and so ( G C D ) = ( C D F ) + ( C G F ) = 6 3 + 2 7 = 9 0 cm 2 .
For (2), we have ( A B D ) = ( G C D ) ( G C A B ) 2 = 9 0 ⋅ ( 3 5 ) 2 = 2 5 0 cm 2 .
Finally, we have ( A B C F ) = ( A B D ) − ( C D F ) = 2 5 0 − 6 3 = 1 8 7 cm 2 . □