A Magic Triangle
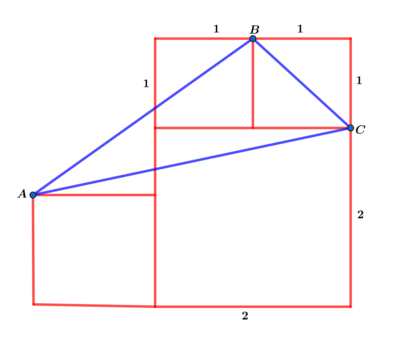
In the four squares above points A , B and C are joined to form △ A B C . Find the area of △ A B C .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
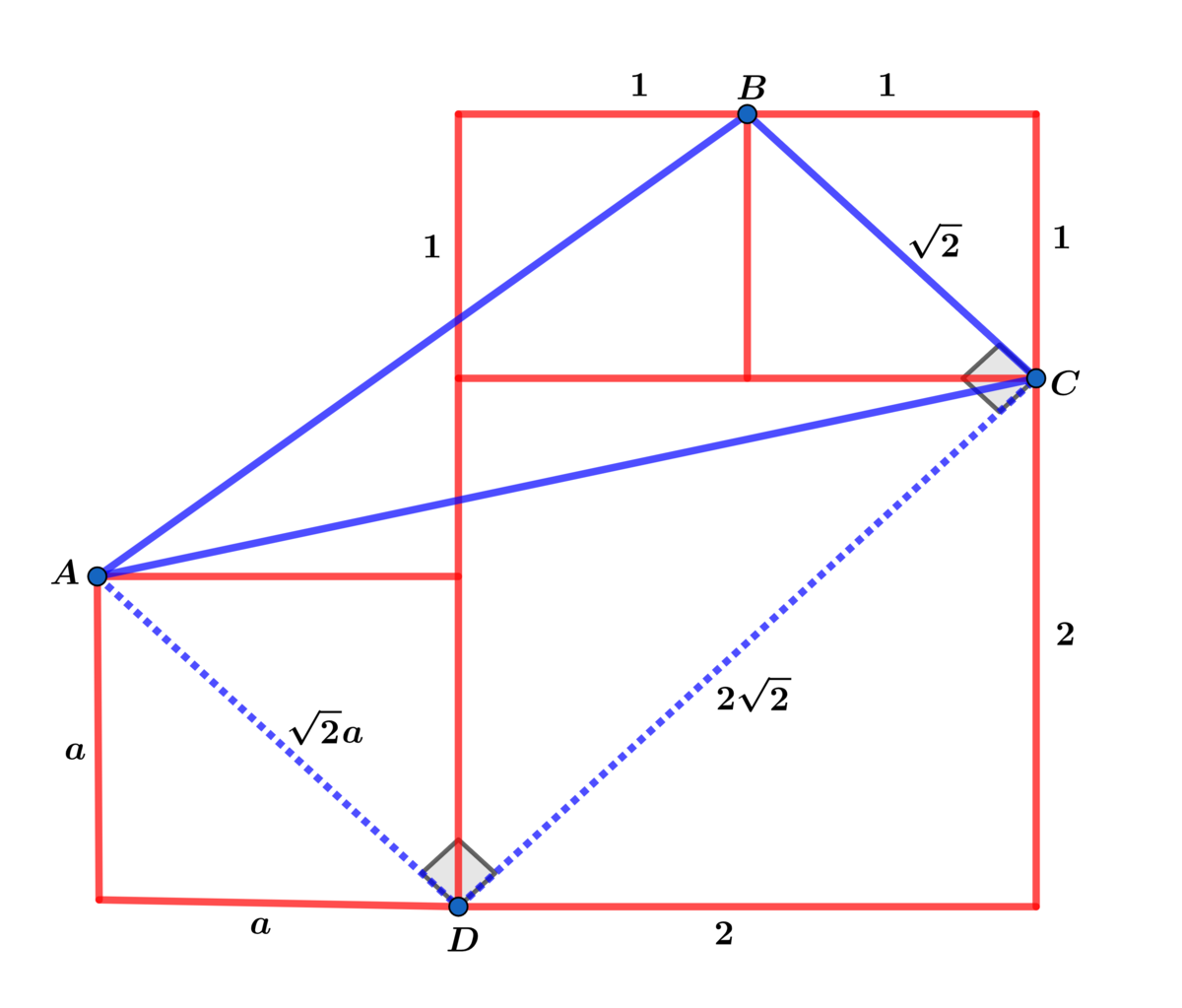
Using the diagram above, the area of the trapezoid A A B C D = 2 1 ( 2 2 ) ( 2 a + 2 ) =
2 a + 2 and the area A △ A D C = 2 1 ( 2 a ) ( 2 2 ) = 2 a
⟹ A △ A B C = A A B C D − A △ A D C = 2 a + 2 − 2 a = 2 .
I did it this way : Let the position coordinates of A be ( 0 , a ) , of B be ( a + 1 , 3 ) and of C be ( a + 2 , 2 ) . Then the area of △ A B C is 2 1 ∣ ( a + 1 ) ( 2 − a ) + ( a + 2 ) ( a − 3 ) + 0 ( 3 − 2 ) ∣ = 2 . Unfortunately I saw the solution before posting my solution.
Let the side length of the bottom left square be a and A be the origin of an x y -plane. Then the coordinates of the vertices of △ A B C are A ( 0 , 0 ) , B ( 1 + a , 3 − a ) , and C ( 2 + a , 2 − a ) . By trapezium rule the area of △ A B C :
[ A B C ] = ( 2 y B + y A ) ( x B − x A ) + ( 2 y C + y B ) ( x C − x B ) + ( 2 y A + y C ) ( x A − x C ) = ( 2 3 − a + 0 ) ( 1 + a − 0 ) + ( 2 2 − a + 3 − a ) ( 2 + a − 1 − a ) + ( 2 0 + 2 − a ) ( 0 − 2 − a ) = 2 3 + 2 a − a 2 + 2 5 − 2 a − 2 4 − a 2 = 2
S means the area of