Launching A Punctiform Object
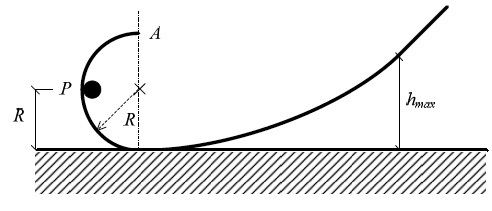
Consider a circular path of radius , when passing through the point the magnitude of the resultant force on the object is , where is the acceleration of gravity.
Find the maximum height that the object reaches the ramp in terms of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The net force acting on the object is resultant of R m ⋅ v 2 and m ⋅ g ⇒ ( R m ⋅ v 2 ) 2 + ( m g ) 2 = 1 7 ⋅ m ⋅ g ⇒ v 2 = 4 ⋅ g ⋅ R thus from W o r k E n e r g y T h e o r e m we get the height achieved by the object from point P as h = 2 ⋅ R So total height achieved by the object is h + R = 3 R . We can design the ramp so that object touches the ramp at its heighest point so it gives h m a x = 3 R