A Matter of Time Riddle

Let the journey time between the stations be $T$ and the gap between trains be $\tau$ . Since the first train from London arrives just as the second train from the village departs, we have $\tau=\frac{T}{2}$ .

Let's say the first train from London departs at time $t=0$ . The first train from the village departs at $t=\frac{T}{2}$ .

When they meet at $t=60$ , the train from London has been travelling for $60$ minutes; the train from the village has been travelling $60-\frac{T}{2}$ minutes. Between them, they have covered the full distance; so

$60+60-\frac{T}{2}=T$

Solving gives $T=\boxed{80}$ .

Let us make a diagram of time lapses of the red London station and blue village station with trains #1 and #2 as colored with the stations they came from (figure not drawn to scale):

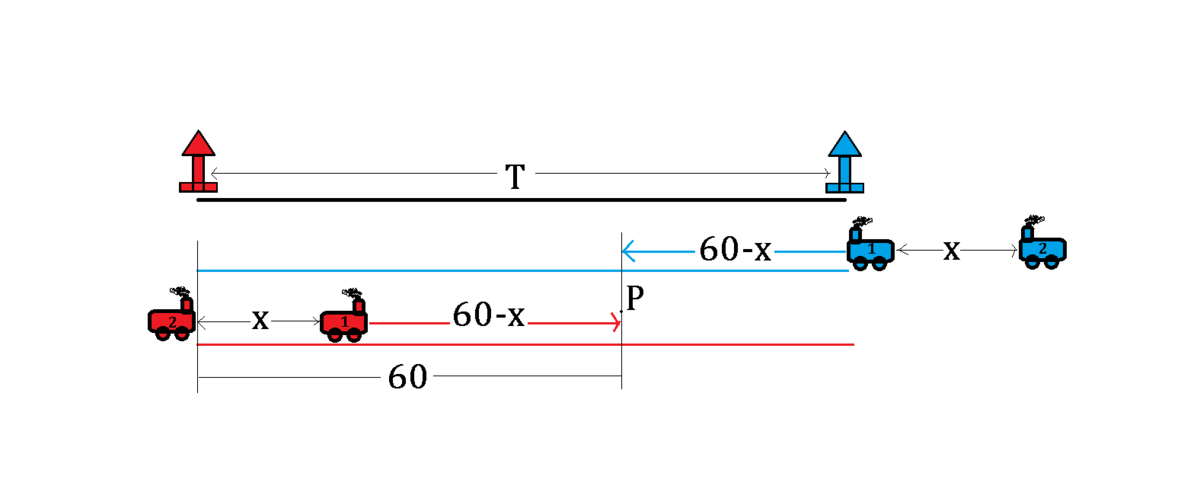
Let $T$ be the total time for this whole trip and $x$ be the time lapse between the consecutive trains. We can see that the first train from the (red) London station has a head start of $x$ minutes when the first blue train starts to move. Then at the meeting point $P$ , which would happen after the first red train left for an hour. At point $P$ , the first blue train had moved for $60-x$ minutes. Thus, we can prove that $T = 60 + 60-x = 120-x$ .

Now let us fast forward to see what would happen at that moment:

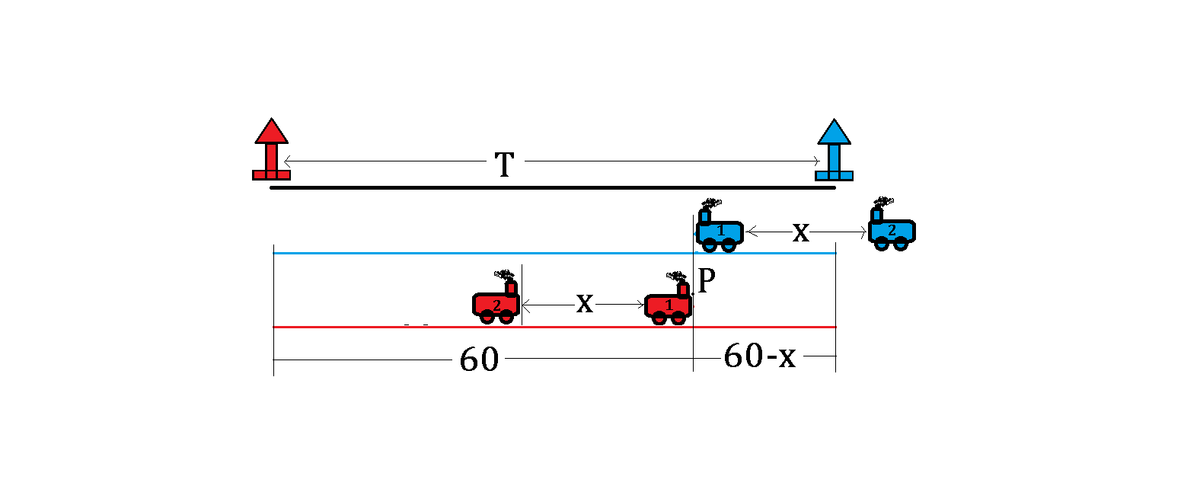
At this point, the first blue train and the red second train would meet after $\dfrac{x}{2}$ minutes because their velocity equals and so reduces the time lapse by half. Meanwhile, the first red train would travel for $60-x$ minutes to reach the destination and meet the second blue train. Thus, the time frame is equal: $\dfrac{x}{2} = 60-x$ .

Solving the equation, we would get: $x = 120-2x$ $3x=120$ $x=40$

Finally, $T = 120 -x =120-40 = \boxed{80}$ minutes.

Let's ignore the details of the train's initial acceleration and assume that they instantly come to full speed.

If we imagine that during most of the day, trains that leave at the same time from both stations must meet halfway, and adjacent departure trains meet in between that time, or 1/4 of the total trip for one train and 3/4 of the trip for the longer traveling train. Otherwise, Holme's and Friend would not have seen a train at all.

Thus, since the train Holmes and Friend is on is the earlier departing train, it must have gone 3/4 of the way in 60 minutes, so 1/4 of the way takes 20 minutes. The total time is 4 x 20 minute or 80 minutes.

Let the travelling time of the trip be $t_r$ and the interval of departure of trains be $t_d$ . The the first train from the village starts $t_d$ after the one Holmes and Wilson are on from London.

As the trains meet 60 minutes after the London train departed, the London train takes 60 minutes to reach the meeting point, while the village train take $60-t_d$ to reach the meeting point. Since the trains are running at the same speed, the distance traveled is directly proportional to time taken, then we have $t_r = 60 + 60-t_d = 120 - t_d \ ...(1)$ (see note below).

As the London train reaches the village the second village train is about to depart. This means $t_r = 2t_d \ ...(2)$ .

Then we have: $120 - t_d = 2t_d$ , $\implies t_d = 40$ and $t_r = 2t_d = \boxed{80}$ minutes.

---

Note: Let the distance between London and the village be $D$ and the speed of the rains be $v$ . Then $t_r = \dfrac Dv$ and 60 minutes after the London train departed,

$\begin{aligned} 60v + (60-t_d)v & = D \\ 60 + 60 - t_d & = \frac Dv \\ \implies t_r & = 120 - t_d \end{aligned}$