A Maximal Square

Geometry Level 5

Let a be the side length of a regular pentagon, and let b be the side length of the largest square that can be inscribed in that pentagon. Find the value of $\lfloor 1000 \frac{a}{b} \rfloor$ .

(The floor function $\lfloor x \rfloor$ gives the greatest integer less than or equal to the real number x .)

The answer is 936.

2 solutions

Anish Puthuraya
Mar 13, 2014

Note : The following figure is the only way I think you could inscribe a square in a pentagon (please tell me it is)

alt text
Considering the above figure,

The angle $\displaystyle\angle BAC$ is clearly $\displaystyle \frac{108^o-90^o}{2} = 9^o$

Hence,
$\angle BCA = 180 - (108+9) = 63^o$

Using Sine Rule in $\displaystyle\Delta ABC$ ,
$\frac{a}{\sin 63^o} = \frac{b}{\sin 108^o}$

Thus,
$\frac{a}{b} = 0.9368$

$\Rightarrow \lfloor 1000\frac{a}{b}\rfloor = \lfloor 936.8\rfloor = \boxed{936}$

Anish, in my opinion that square is not inscribed in the pentagon because the bottom corner is not contact with the base of pentagon. As far as I know, the term 'inscribed' means all the vertices must lie on the sides of outer shape. It should be like this:

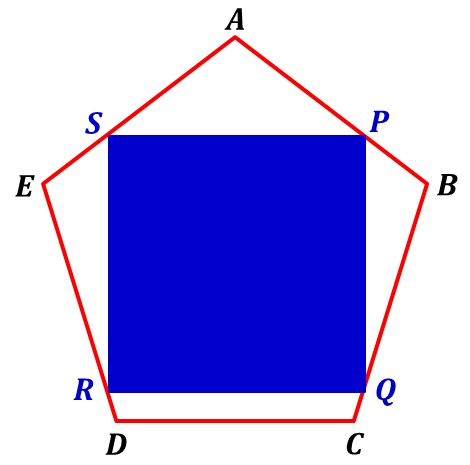Square in Pentagon

Tunk-Fey Ariawan - 7 years, 2 months ago

I dont think it can be done. I searched everywhere for the above figure, but instead, I only found the one that I used in my solution.

Are you certain that the above shape that you drew is a square? (I do not mean any suspicion)

Anish Puthuraya - 7 years, 2 months ago

Geez, my bad Anish. Your solution is correct. Indeed, $PQRS$ in my picture is a square but it doesn't yield the maximum area of square like yours. I don't know some how my answer is 'correct' although it's not the correct answer. Lucky me. :D

Tunk-Fey Ariawan - 7 years, 2 months ago

it isn't the largest square

Chandra Shekhar - 7 years, 1 month ago

Tunk-Fey, your suggestion does not give the maximum area. It's off by about 4.8% of the maximum. I checked it out on AutoCAD.

Renato Javier - 7 years, 2 months ago

but you must give a reason why it is so?

akash omble - 7 years, 3 months ago

good.

Renato Javier - 7 years, 3 months ago

well done

Malay Pandey - 7 years, 3 months ago

i thought it was mixed fraction. :'( question should be written clearly.

Shahbaz Patel - 7 years, 2 months ago

This square is not inscribed in the pentagon. All four corners of the square have to lie on the pentagon, for it to be truly inscribed.

Hosam Hajjir - 7 years, 2 months ago

Nice solution

Mardokay Mosazghi - 7 years, 1 month ago

Swapnil Tyagi
Mar 19, 2014

b/sin108=a/sin63 in the triangle formed by taking one of corners of largest square as corners of pentagon . a/b=sin63/sin108. 1000a/b=936.85 gif=936

I agree that inscribed should mean all edges lie on the curve. For the sake of Mathematics, this problem should explicitly state the fact of a common edge .

Rajen Kapur - 7 years, 2 months ago

I would like to see a proof that this is the maximum.

Dobromir Dimitrov - 7 years, 1 month ago

A Maximal Square

The answer is 936.

2 solutions

0 pending reports