A classical mechanics problem by Mardokay Mosazghi
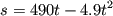 A stone projected upwards has its equation of motion given by:
where s is in meters and t in seconds.
What is the maximum height reached by the stone?
A stone projected upwards has its equation of motion given by:
where s is in meters and t in seconds.
What is the maximum height reached by the stone?
The answer is 12250.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Hey yo,
As the height is max,means that the rate of height is 0,
s = 490t - 4.9t^2 ds / dt = 490 -9.8t = 0
t =490 / 9.8 = 50s
therefore, maximum height is = 490(50) - 4.9(2500) = 12 250 m...
thanks yo....
From the equation , we can derive that the value of u , that is initial velocity is 490 m/s .
Therefore by using the formula to calculate the maximum height , that is u^2 /2g , which gives s the answer as 12250
You do not need calculus for this.
The y coordinate of the vertex of a parabola is
− 4 a b 2 − 4 a c
In this case:
− − 1 9 . 6 4 9 0 2 = 1 9 . 6 2 4 0 1 0 0 = 1 2 2 5 0
first of all differentiate the given equation to zero......find the value of t.........put the value of t in the equation...nd u reach to the problem's answer!!!
For this problem, you don't necessarily need differentiation. You just need some simple understanding of gravity. First of all, if you assume that air resistance is negligible, that would mean that the time taken for the ball to go up is the same as the time taken for it to go down. This means that you can assume the displacement to be 0 and you can solve for t=100, where it is the total time taken for the ball to go up and go down. Divide 100 by 2 and substitute the time into the equation given and you get 12250.
The velocity, v, is found by differentiating the above equation with respect to t.Then you get ds/dt=v=490-9.8t When the stone reaches the highest point, its upward motion stops. Hence, v = 0. so 0=490-9.8t) solve for t which is 50 now the maximum height can be found by substituting t = 50 seconds into the original equation of motion 490(50)-4.9(50^2) =12250 Hence, the maximum height reached by the stone thrown upwards is 12,250 meters.