Precarious cylinders
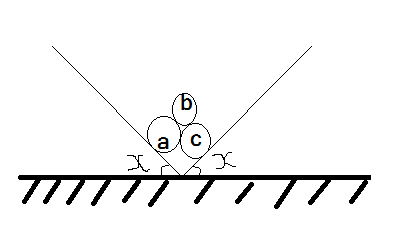
Three identical rigid circular cylinders A , B and C are arranged on smooth inclined surfaces as shown.
The least value of that prevent the arrangement from collapsing can be expressed as , where and are positive integers with coprime.
Submit your answer as .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The picture doesn't quite look like it, but I assumed that the system is bilaterally symmetrical.
The centers of the three cylinders make an equilateral triangle, and so the the normal force between the top cylinder and the bottom two is 60 degrees from the horizontal. Thus, if we call the magnitude of the normal force between the top and (one of) the bottom cylinders F N 1 then the horizontal force from the top cylinder on (one of) the bottom cylinders is F N 1 sin ( 6 0 de g ) = 2 1 F N 1
We are looking for the minimum angle which leads to equilibrium: this implies that the normal force between the bottom two cylinders is zero. Thus we can equate the horizontal components of the normal force between the top and bottom cylinders with that of the surface and the bottom cylinder (I will call the normal force between the surface and bottom cylinder F N 2 ) and so we get:
2 1 F N 1 = F N 2 sin ( x )
We can replace the magnitude of the normal forces with the constraints that the vertical components need to balance the forces of gravity. Let us call the mass of a single cylinder M . Twice the vertical component of F N 2 will then equal the weight of all three cylinders, 3 M g . (We multiply by two because the force F N 2 is acting on both of the bottom cylinders.) So we get:
2 F N 2 cos ( x ) = 3 M g .
Similarly, twice the vertical component of F N 1 will need to balance the weight of the top cylinder, so we get:
3 F N 1 = M g
Combining these two weight-constraints with the original constraint in such a way that F N 1 and F N 2 are eliminated, we get:
x = t a n − 1 3 3 1 = t a n − 1 3 3 / 2 1