Arrangement in motion
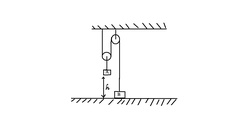 In the arrangement shown in figure, the mass of the body A is 4 times that of body B. The height h=20 cm . At a certain instant, the body B is released and the system is set in motion. What is the maximum height (in cm), the body B will go up? Assume enough space above B and A sticks to the ground. (
g
=
1
0
m
s
−
2
)
In the arrangement shown in figure, the mass of the body A is 4 times that of body B. The height h=20 cm . At a certain instant, the body B is released and the system is set in motion. What is the maximum height (in cm), the body B will go up? Assume enough space above B and A sticks to the ground. (
g
=
1
0
m
s
−
2
)
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
most people would forget the vertical motion after the string becomes slack.
Nice !! But I used Energy conservation by using constrained equation rapidly ! It is much less calculating ! In fact I solved it orally :)
Can you please explain why 2 a B = a A ? I was expecting equal values.
Log in to reply
When two strings are connected to one pulley, the effective s of thread it 2 × s of pulley.
⇒ 2 s A = s B
Differentiating twice, 2 a A = a B
This question came in Problems in General Physics by I E Irodov
Q.No: 76 Physical Fundamentals of Mechanics.
Solution
4 m g − 2 T 2 T − 2 m g ⇒ a = 4 g s 2 h a 2 g Velocity when v 2 And further, h ′ ⇒ H = 3 h = 4 m a = 4 m a the other block touches the floor is = 2 g h = h
Found another solution online: (it uses energy conservation) http://irodovsolutionsmechanics.blogspot.in/2007/08/irodov-problem-176.html
We'll work in S.I. and then finally covert our answer to C.G.S..
Let m A = 4 m B = 4 m (say). Let tension in the string while it is taut be T From constraint relations 2 a B = a A = a (say).
Then Newton's second law yields
T − m g = 2 m a − − − ( i )
4 m g − 2 T = 4 m a − − − ( i i )
Now 2 × ( i ) + ( i i ) gives
a = 4 g .
So for motion of A till it hits ground after which string becomes slack( → T = 0 ) due to sticking, we have
5 1 = 2 1 ⋅ a ⋅ t 1 2 → t 1 = 5 g 8 .
During this time B travels a distance d 1 = 2 1 ⋅ 2 a ⋅ t 1 2 = 5 2 .
At this point velocity of B v = 2 a ⋅ t 1 = 5 2 g . After this T = 0
→ d 2 = 2 g v 2 = 5 1 .
So total distance moved by B is d = d 1 + d 2 = 5 3 m = 6 0 c m .