A classical mechanics problem by Pankaj Joshi
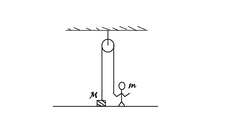 In the figure, the block of mass M (=10 kg) is at rest on the floor. The minimum acceleration with which a boy of mass m (=2 Kg) should climb along the rope of negligible mass so as to lift the block from the floor is (
g
=
1
0
m
/
s
2
):
In the figure, the block of mass M (=10 kg) is at rest on the floor. The minimum acceleration with which a boy of mass m (=2 Kg) should climb along the rope of negligible mass so as to lift the block from the floor is (
g
=
1
0
m
/
s
2
):
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
IF somebody can explain please because Im totally messed up right now,what I thought is 50 ms^-2 the right answer,Please explain
Log in to reply
If the boy hangs on the rope, he will exert 20 N force which is not sufficient to rise the 10 kg mass.It requires 100 N force. The additional 80 N force is obtained by accelerating upwards with 40 m/s^2.
Same is the case here...
Really nice solution sir.
I don't think (from where the boy stands) that he should climb up along the rope , but instead he should perform an acceleration of (40 m/s^2) by pulling the rope downwards while he is hanging .. Please anyone correct me if I'm wrong ??
Using F=mg, (Newton's 2nd law)
Left side; 10 kg x 10 m/s² = 100 N
Right side, mass of the climber x g =
2 kg x 10 m/s² = 20 N
So if I need 80 N more with a climber of a mass of 2 kg,
80 N / 2 kg = 40 m/s²
Of course, a little more acceleration will be needed to lift the block as 40 m/s² is what needed to keep the system in balance.
T tension G gravity F total
On the Left side: F = T − G = m ⋅ a = 0 N Then T = G = 1 0 ⋅ 1 0 = 1 0 0 N On the Right side: F = T − G = m ⋅ a Then a = m T − G = 2 1 0 0 − 2 ⋅ 1 0 = 4 0 m / s 2
when the boy hangs on the rope, he exerts a force of 20 N. To lift the block 100 N force is required. The additional force of 80 N if provided by accelerating with 40 m/s^2.