A mere square
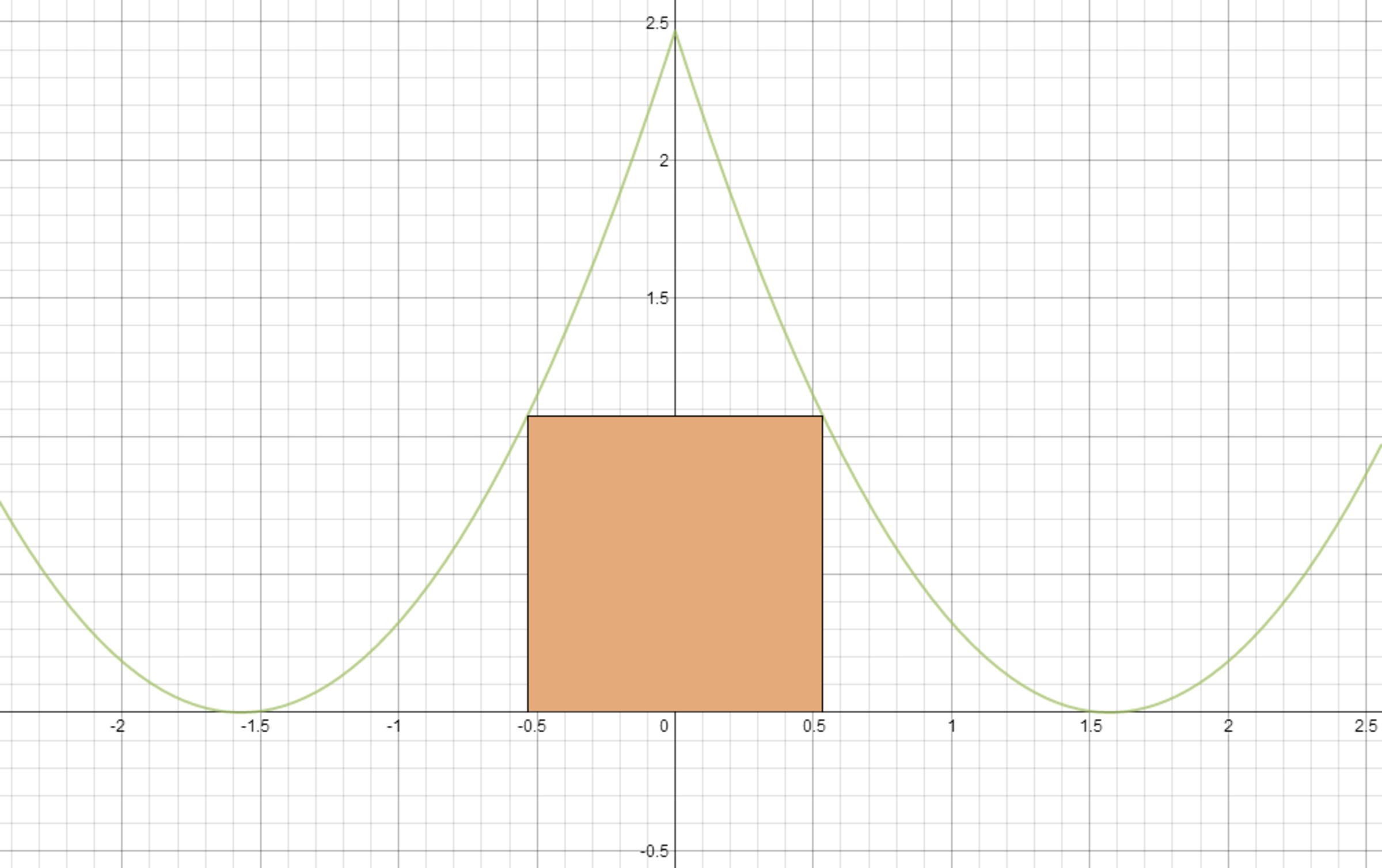
The following shown here is a portion of the graph for f ( x ) = ( arcsin cos x ) 2 . In each region bound by the x -axis and f ( x ) , a square can be drawn, with its top two vertices touching f ( x ) , and its bottom two vertices touching the x -axis, as pictured.
Considering the periodic properties of f ( x ) , the area of any of these squares can be expressed in the form π A + B π + B − C ( π + A ) π + D with A a prime number, B a perfect cube, and C and D perfect squares. Find C ⋅ D A ⋅ B .
This problem is original. The picture of the graph was produced from Desmos and the orange square was added with Microsoft Paint.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We note that the vertex of the square in the positive quadrant must be of the form a , 2 a and 0 < a < 2 π .
f ( a ) ⇒ ( sin − 1 ( cos a ) ) 2 sin − 1 ( cos a ) cos a ⇒ sin a ⇒ cot a ⇒ 2 π − a a 2 − ( π + 2 ) a + 4 π 2 ⇒ a ⇒ a = 2 a = 2 a = 2 a = sin ( 2 a ) = 1 − sin 2 ( 2 a ) = cos ( 2 a ) = tan ( 2 a ) = 2 a = 0 = 2 π + 2 ± ( π + 2 ) 2 − π 2 = 2 π + 1 − π + 1 The other solution is > 2 π and rejected.
The area of the square is 4 a 2 = π 2 + 8 π + 8 − 4 ( π + 2 ) π + 1 . ⇒ C D A B = 4 × 1 2 × 8 = 4
The rightmost part of the function f ( x ) = ( arcsin cos x ) 2 for x ≥ 0 is equal to g ( x ) = ( x − 2 π ) 2 on the interval [ 0 , π ] .
Let's look at these four points: ( 0 , 0 ) , ( a , 0 ) , ( a , g ( a ) ) , and ( 0 , g ( a ) ) . When connecting the points we see a rectangle. The height of the rectangle is g ( a ) and the length is a . We want some value of a such that the horizontal distance D 1 from ( 0 , g ( a ) ) to ( a , g ( a ) ) is equal to half the vertical distance D 2 from ( a , 0 ) to ( a , g ( a ) ) .
We can readily see that D 1 = a and D 2 = g ( a ) , and so we want to solve the equation
D 1 = 2 D 2 ⇒ a = 2 1 ( a − 2 π ) 2 .
This is simply a quadratic with a solution of
a = 1 + 2 π ± 1 + π
However, the only feasible solution here is 1 + 2 π − 1 + π , and this is the value of the side of the square. Now we want to find the area of this square and it is
a 2 = 4 π 2 + 2 + 2 π − ( 2 + π ) 1 + π , so A = B = 2 , and C = D = 1 and C D A B = 4
This is where I'm stuck. My solution is of the form 4 π A + B π + B − C ( π + A ) π + D and the OP's form is π A + B π + B − C ( π + A ) π + D .
I don't understand why I differ from the OP's form. Can anyone explain?
Please note that in your solution the length of side of square will be D 2 which is 2 D 1 = 2a. So area of square will be (2a)² =4a²
I actually made the same mistake when I first posted this problem! The area of the square is ( 2 a ) 2 = 4 a 2 instead of simply a 2 , since a is the length of half a square. Thus, the area one would calculate using only a 2 is one-quarter of the required area.
First note that as cos ( x ) is an even function, arcsin ( cos ( x ) ) will be even as well. Also note that arcsin ( cos ( 0 ) ) = arcsin ( 1 ) = 2 π and that arcsin ( cos ( 2 π ) ) = arcsin ( 0 ) = 0 . Further, on the interval 0 ≤ x ≤ 2 π we have that arcsin ( cos ( x ) ) = arcsin ( sin ( 2 π − x ) ) = 2 π − x .
Thus the square in question will have its upper right corner touching the curve y = ( 2 π − x ) 2 , and by the symmetry of f ( x ) this corner will have coordinates ( a , 2 a ) where a is such that
2 a = ( 2 π − a ) 2 ⟹ 8 a = ( π − 2 a ) 2 = π 2 − 4 π a + 4 a 2 ⟹ 4 a 2 − ( 4 π + 8 ) a + π 2 = 0
⟹ a = 8 4 π + 8 ± ( 4 π + 8 ) 2 − 1 6 π 2 = 8 4 π + 8 ± 4 ( π + 2 ) 2 − π 2 = 2 π + 1 ± π + 1 .
Now as we require that a ≤ 2 π we take the negative root, i.e., a = 2 π + 1 − π + 1 .
The area of the desired square is then ( 2 a ) 2 = ( π + 2 − 2 π + 1 ) 2 =
( π + 2 ) 2 + 4 ( π + 1 ) − 4 ( π + 2 ) π + 1 = π 2 + 8 π + 8 − 4 ( π + 2 ) π + 1 .
Thus C D A C = 4 ∗ 1 2 ∗ 8 = 4 .