A nice answer!

Extend the red circles above to an infinite number of circles.
For each integer n ≥ 1 , circle w n is tangent to w n − 1 and tangent to diameter A B . of the semicircle.
Let S be the sum of all the radii of the red circles and R be the radius of the semicircle.
Find R 2 S
The answer is 1.61803398875.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
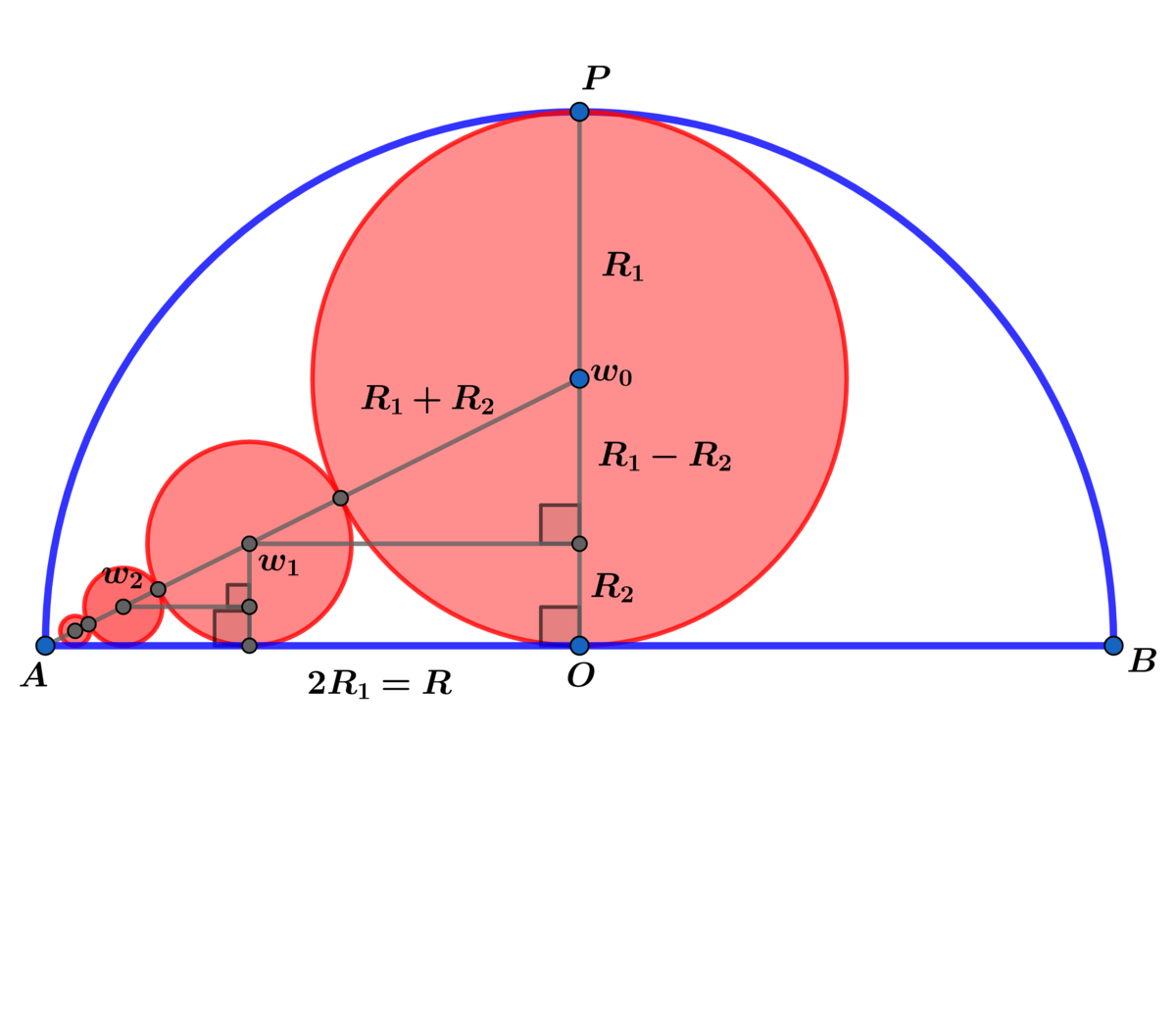
A w 0 = 5 R 1 ⟹ 5 = R 1 − R 2 R 1 + R 2 ⟹ ( 5 − 1 ) R 1 = ( 5 + 1 ) R 2 ⟹
R 2 = 5 + 1 5 − 1 R 1 and 5 = R 2 − R 3 R 2 + R 3 ⟹ R 3 = 5 + 1 5 − 1 R 2 = ( 5 + 1 5 − 1 ) 2 R 1
In General R n = ( ϕ ϕ − 1 ) n − 1 R 1 ⟹ S = R 1 ∑ n = 1 ∞ R n = ϕ R 1 = 2 ϕ R ⟹
R 2 S = ϕ ≈ 1 . 6 1 8 0 3 3 9 8 8 7 5
Nice problem and solution! You should specify that S is the sum of the radii of all the red circles.
Let R = 1 and label C and D as follows:
Then P D = D O = C D = 2 1 , and by the Pythagorean Theorem on △ A D O , A D = A O 2 + D O 2 = 1 2 + ( 2 1 ) 2 = 2 5 .
Then A C = A D − C D = 2 5 − 2 1 = 2 5 − 1 .
The sum of the radii of all the red circles is S = 2 1 A C + C D = 2 1 ⋅ 2 5 − 1 + 2 1 = 4 5 + 1 .
Therefore, R 2 S = 1 2 ⋅ 4 5 + 1 = 2 5 + 1 = ϕ ≈ 1 . 6 1 8 .