A nice Diophantine equation (if such exists)

Number Theory Level pending

How many positive integer triplet ( x , y , z ) (x, y, z) solutions are there to the equation below

x 11 + 143 y 11 + 25 z 11 = 232 3 6 + 12 x^{11} + 143y^{11}+25z^{11} = 2323^6+12

If there are any solutions, what are they?

Two - (-19912, 7777, 16237); (-19912, -9991, 23232) Only one: (69, 23, 56) This equation has no solutions Only one: (68, 44, 51)

Bojan Dimovski by Bojan Dimovski , 17, Macedonia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Bojan Dimovski
Jul 11, 2017

By Fermat's Little Theorem, we have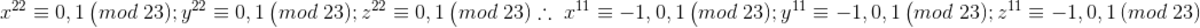 Now, 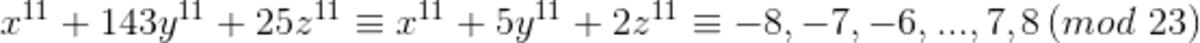On the other hand, we have 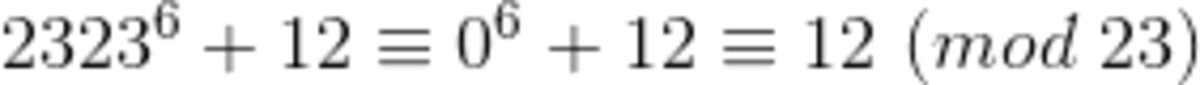But 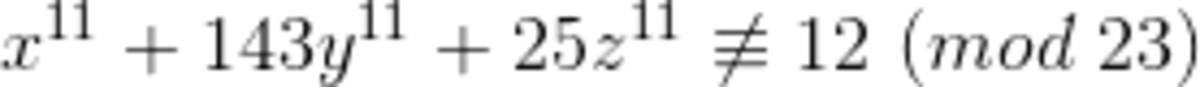The L.H.S and R.H.S should be equal and therefore have the same congruence in any modulo, but they do not, so they are also not equal, from which we conclude that there are no positive integer solutions to (x, y, z).

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...