A nice problem from the 2018 September CSAT mock test

I solved this problem by using graphs.

Given that $f(x)$ has a global minimum of $0$ . It means that $x-$ axis will touch the curve $y=f(x)$ .

Let it touch the curve at $x=a$ . Then, $f(x)=\frac{1}{2}(x-a)^{2}(x^{2}+bx+c)$ .

Both roots of the quadratic equation $(x^{2}+bx+c)$ either be imaginary or any positive real number ( lets say $d$ ).

Now $a$ is the root of $f(x)=0$ then the roots of $g(x)=a$ will be the roots of $h(x)=0$ .

$x^{4}e^{-x}=a$ .

$x^{4}=a e^{x}$

$a>0$

drawing the curve $y=x^{4}$ and $y=a e^{x}$ .

From graph we can say that equation $g(x)=a$ has three roots. Now one more needed to satisfy the 1st condition.

For that $b=c=0$ or $d=0$ . Then $f(x)=\frac{1}{2}x^{2}(x-a)^{2}$ and its graph will be

[One more possibility is that $g(x)=a$ has two roots when both curve touch at some point

In that case we need two such $a$ 's then only we can have four roots for $h(x)=0$ .

$4 x^{3}=a e^{x}$ ( same slope )

$x^{4}=a e^{x}$ (same point)

from these two equation

$a=0$ (but $a>0$ )

and $a=(\frac{4}{e})^4$

so $a$ has only one possible value but we needed two.]

For 3rd condition $f(x)=8$ should have two positive roots. and graph for $y=f(x)-8$

The curve will touch $x-$ axis at point $x=\frac{a}{2}$ . Then

$f(\frac{a}{2})=8$

$\frac{1}{2}(\frac{a}{2})^{2}(\frac{a}{2}-a)^{2}=8$ .

$\frac{a}{2}=+-2$

$a=+-4$

$f'(x)=x(x-a)(2x-a)$

So $f'(5)=5(5-4)(2\times 5-4)$

$f'(5)=30$

Assume $f,\:g,\:h$ are real-valued functions. Before we tackle $h(x)=f(g(x))$ , let's find out what the argument $g(x)$ looks like.

---

Analyzing $g(x)$

We immediately notice $g(x)\geq 0$ , and $x=0$ is its only zero - it is a global minimum! We calculate the first two derivatives and check the limits $x\rightarrow \pm\infty$ to get a general idea what $g(x)$ looks like: $\begin{aligned} g^{(1)}(x)&=-2x^3(x-4)e^{-x}, &&&g^{(2)}(x) &= 2x^2[(x-4)^2-4]e^{-x}, &&&&& \lim_{x\rightarrow -\infty}g(x)&=+\infty, &&&\lim_{x\rightarrow +\infty}g(x)&=0^+ \end{aligned}$ We check for additional extrema and ignore $x=0$ , because we already know it's a minimum: $\begin{aligned} g^{(1)}(x) &= 0 &&&\Rightarrow &&&& x&=4, &&&&& g^{(2)}(4)&=-128e^{-4}<0 &&&\Rightarrow &&&&\text{local maximum!} \end{aligned}$ We finally check the value of the local maximum and are then able to plot the function: $g(4)=512e^{-4} > \frac{512}{3^4}=\frac{512}{81}>6>4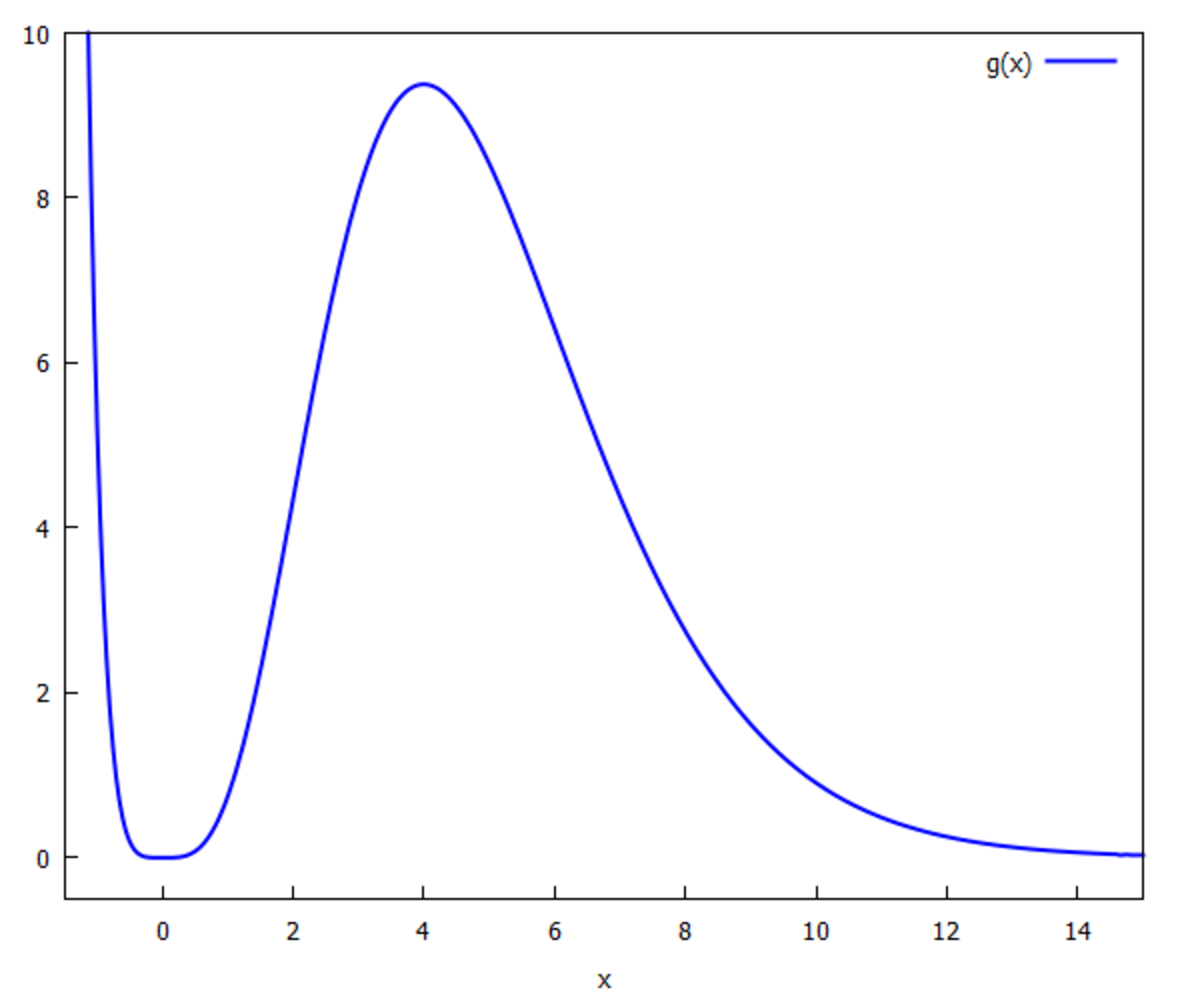$ We note: The equation $g(x)=c\geq 0$ can only have one, two or three distinct solutions!

---

Analyzing $f(x)$

By definition, $f$ is a degree four polynomial with four zeroes $x_k$ . One of them, let's call it $x_1$ , is also a (global) minimum: $\begin{aligned} f(x_1)=f^{(1)}(x_1)&\overset{!}{=}0 &&&\Rightarrow &&&& f(x)&=\frac{1}{2}(x-x_1)^2(x-x_2)(x-x_3) \end{aligned}$ The other two zeroes cannot be distinct reals, because then $f$ would return negative values between them - they must be either equal or complex conjugates! We now have the form $f(x)=\frac{1}{2}(x-x_1)^2\left[(x-a)^2+b^2\right],\qquad b^2\geq 0$ We note: $f$ can have either one or two distinct real zeroes!

---

Analyzing $h(x)$

By the above, we know $f$ can only have one or two real zeroes. If it had only $x_1$ , the first condition would be violated: $\begin{aligned} h(x)=f(g(x))&\overset{!}{=}0 &&& \Rightarrow &&&& g(x)&\overset{!}{=}x_1 &\text{has at most three distinct solutions} \end{aligned}$ This contradicts the condition that we should find four distinct solutions! We need $f$ to have two non-negative zeroes, i.e. $\begin{aligned} f(x)&=\frac{1}{2}(x-x_1)^2(x-a)^2, &&& 0&\leq x_1<a \end{aligned}$

---

Let's check the second condition. A sign-table (or a quick sketch of $f(x)$ ) shows that for $x_1>0$ , the composite function $h(x)$ will always have a local maximum at $x=0$ - contradiction! We need to have $x_1=0$ : $\begin{aligned} f(x) &=\frac{1}{2}x^2(x-a)^2, &&& 0&<a<\red{g(4)} &&&&&\left| \text{local maximum at } x=\frac{a}{2}\text{ with }f(a/2)=\frac{a^4}{32} \right. \end{aligned}$ With $x_1=0$ , we notice for $a\geq \red{g(4)}$ the composite has (at most) three zeroes - contradiction! Now, $h$ even has a global minimum at $x=0$ .

---

The third condition is the trickiest: $\begin{aligned} h(x)=f(g(x))&\overset{!}=8 &&&\Rightarrow &&&& (*)&& f(y)&\overset{!}{=}8 &&&\wedge&&&&(**)&& g(x)&=y \end{aligned}$ The equation $f(y)=8$ can have two, three or four distinct solutions, depending on $0<a<4,\:a=4$ and $4<a<g(4)$ , respectively. One of the solutions is always negative and will not satisfy the second equation, so we discard it. We're left with one, two and three solutions, respectively.

If $0<a<4$ , the only remaining solution of $(*)$ yields (at most) three solutions in $(**)$ , just like before - contradiction! If $4<a<g(4)$ , the three remaining solutions of $(*)$ lead to (at least) seven solutions in $(**)$ - contradiction!

That leaves the case $a=4$ that indeed satisfies all conditions. The answer is $\begin{aligned} f^{(1)}(x)&=x(x-4)(2x-4)&&&\Rightarrow &&&& f^{(1)}(5)&=\boxed{30} \end{aligned}$