A nice simple harmonic oscillator
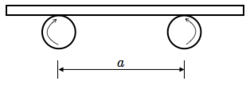 Two parallel cylinders spin in opposite directions as shown. The distance between the center of the cylinders is
m . A straight uniform bar of length
rests on the cylinders. The coefficient of kinetic friction between the bar and a cylinder is
. Find the period of the oscillations that result from displacing the bar from its equilibrium position, in seconds.
Two parallel cylinders spin in opposite directions as shown. The distance between the center of the cylinders is
m . A straight uniform bar of length
rests on the cylinders. The coefficient of kinetic friction between the bar and a cylinder is
. Find the period of the oscillations that result from displacing the bar from its equilibrium position, in seconds.
Use m/s .
The answer is 4.44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the left and right cylinders exert a normal force of N 1 and N 2 on the bar and have an x-coordinate of − 2 a and 2 a respectively.
Since the bar does not move vertically, there is no net vertical force. N 1 + N 2 = m g
Since the bar does not spin, there is no net torque about its centre of mass. When the centre of mass of the bar has a displacement of x away from the equilibrium position, N 1 ( d + x ) = N 2 ( d − x )
Considering horizontal forces, μ N 1 − μ N 2 = − k x
From SHM we know that T = 2 π k m
Solving these 4 equations for 4 unknowns, T = 2 π 2 μ g a