Climbing up the social ladder
x x 4 = 4 , x x 2 + x x 8 = ?
x is a real number.
The answer is 258.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Can you prove that y y = 4 4 has a unique solution for y ?
In response to Challenge Master
:
If
x
x
=
n
n
⇒
x
n
1
=
n
x
1
.
Thus, we need to find the points of intersection of the curves
y
=
x
n
1
and
y
=
n
x
1
. By studying the
graph
, we can conclude that there is a unique point of intersection of all positive integral values of
n
. At
n
=
4
, the graph looks like this.
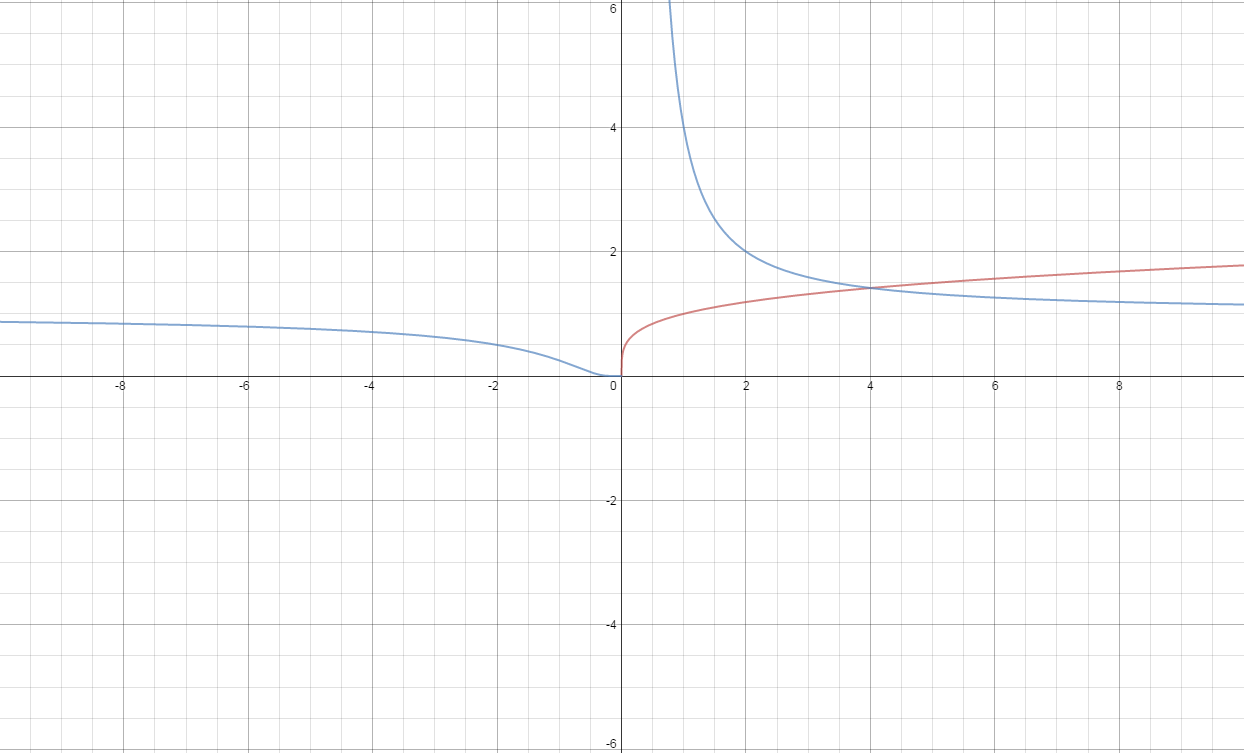 graph
graph
Log in to reply
You don't need to use graph. Note that f ( x ) = x x is a strictly increasing function for x > 1 so it's one-to-one relation thus there's only one value of x for x x = 2 5 6 , namely x = 4 .
Log in to reply
Exactly! Actually It came to my notice after I posted the comment. :P
This is one of the Pre-RMO problem, click here to see the discussion.
So I can equally just go ahead with: Notice that 2 2 4 = 4 = x x 4 , hence x = 2 ? :)
This is A Pre RMO Problem. I liked it.
Simple,
Let y = x x x x ⋯
x y x x y Let y ⇒ x x 4 ⇒ x 4 ⇒ x x x 2 x x 8 = y = y = 4 = 4 = 4 = 2 2 1 = x 2 = 2 = x 2 4 = x 1 6 = 2 8 = 2 5 6
∴ x x 2 + x x 8 = 2 5 8
x^16=2^8 Typos found.
That is very clever!
x = a 2 1 x x 4 = a 2 a 2 = ( a a 2 ) 2 1 = 4 ⇒ a a 2 = 1 6
It's easy to see a = 2. Substituting back in gives us the correct value for x, which is 2 .
x x 4 = x x ∗ x x ∗ x x ∗ x x = ( 2 ) 4 . x = 2 . . . . . . . . . . . E x p . = 2 + 2 5 6 = 2 5 8
That is not how exponents work. Note that ( x x ) 4 = x ( x 4 ) .
an ingenuous and mistaken coincidence... unhappily too close of a non polite consideration...
Please verify your solution. You just got the answer through luck.
Try this problem. Good luck with guessing.
Let y = x 4 . Then we have x x 4 = x 4 ˙ 4 x 4 = y 4 y = 4
⟹ y y = 4 4 ⟹ y = x 4 = 4 ⟹ x = ( 2 2 ) 4 1 = 2
⟹ x x 2 + x x 8 = 2 2 2 + 2 2 8 = 2 2 + 2 1 6 = 2 + 2 8 = 2 5 8
In response to Moderator's note: We note that d y d y y = ( ln y + 1 ) y y > 0 for y > e 1 . Implying that y y is an increasing function for y > e 1 . This means that y y = k has an unique solution when k > e e 1 1 .