RMO 2014
Let x 1 , x 2 , … , x 2 0 1 4 be positive real numbers such that j = 1 ∑ 2 0 1 4 x j = 1 . Determine the smallest constant K , such that K j = 1 ∑ 2 0 1 4 1 − x j x j 2 ≥ 1 .
This problem is taken from RMO 2014.
The answer is 2013.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Same Solution. And problem need edition.
Same Way!!
Also can be done by M.S-A.M-G.M-H.M
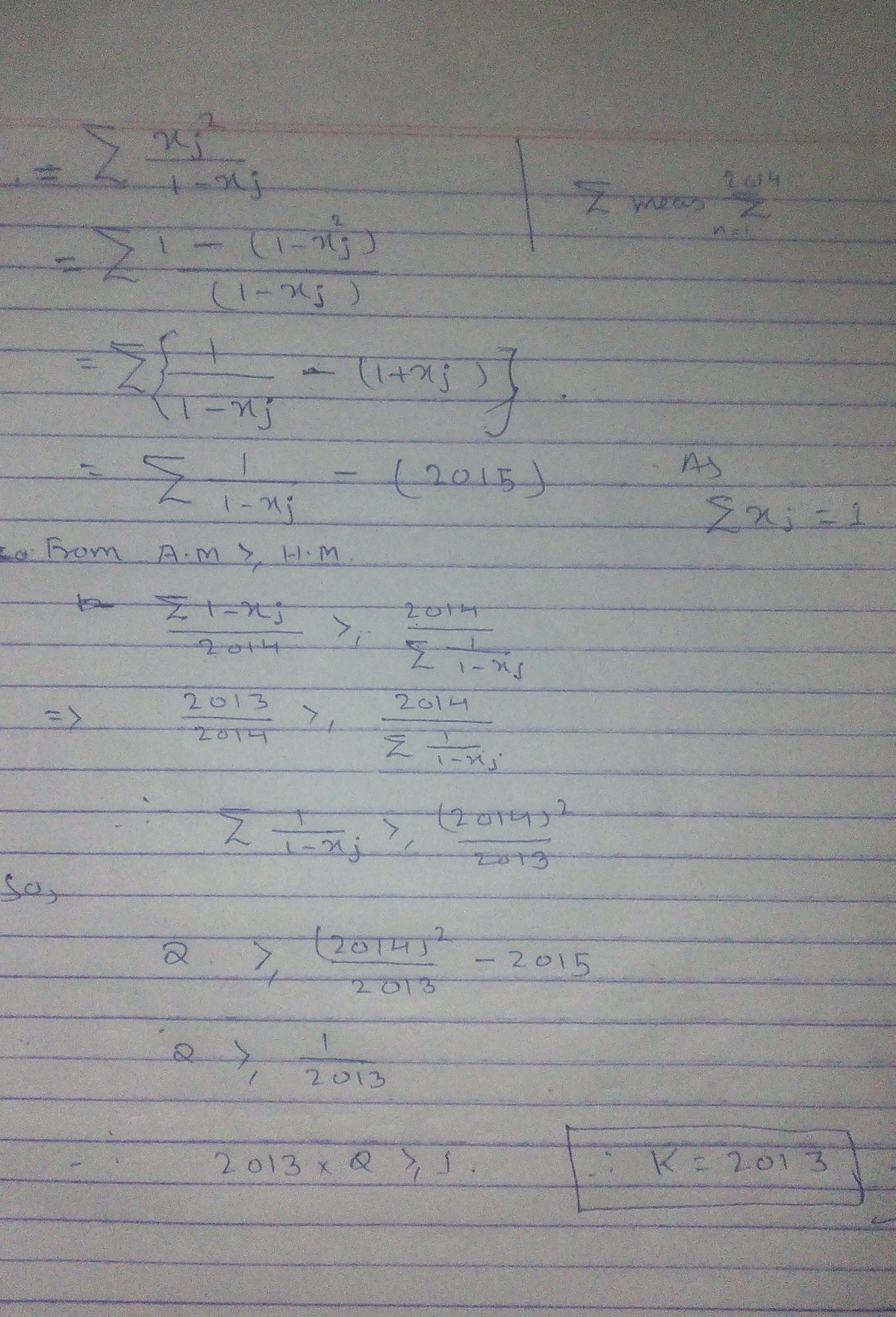
Nihar Mahajan , please edit the question to
K j = 1 ∑ 2 0 1 4 1 − x j x j 2 ≥ 1
By Cauchy-Schwarz Inequality/Titu's lemma, we have
j = 1 ∑ 2 0 1 4 1 − x j x j 2 ≥ ∑ j = 1 2 0 1 4 ( 1 − x j ) ( ∑ j = 1 2 0 1 4 x j ) 2 ≥ 2 0 1 4 − ∑ j = 1 2 0 1 4 x j 1 ≥ 2 0 1 3 1 2 0 1 3 j = 1 ∑ 2 0 1 4 1 − x j x j 2 ≥ 1
this gives the smallest value of constant 2 0 1 3 .