CrossNumber Puzzle
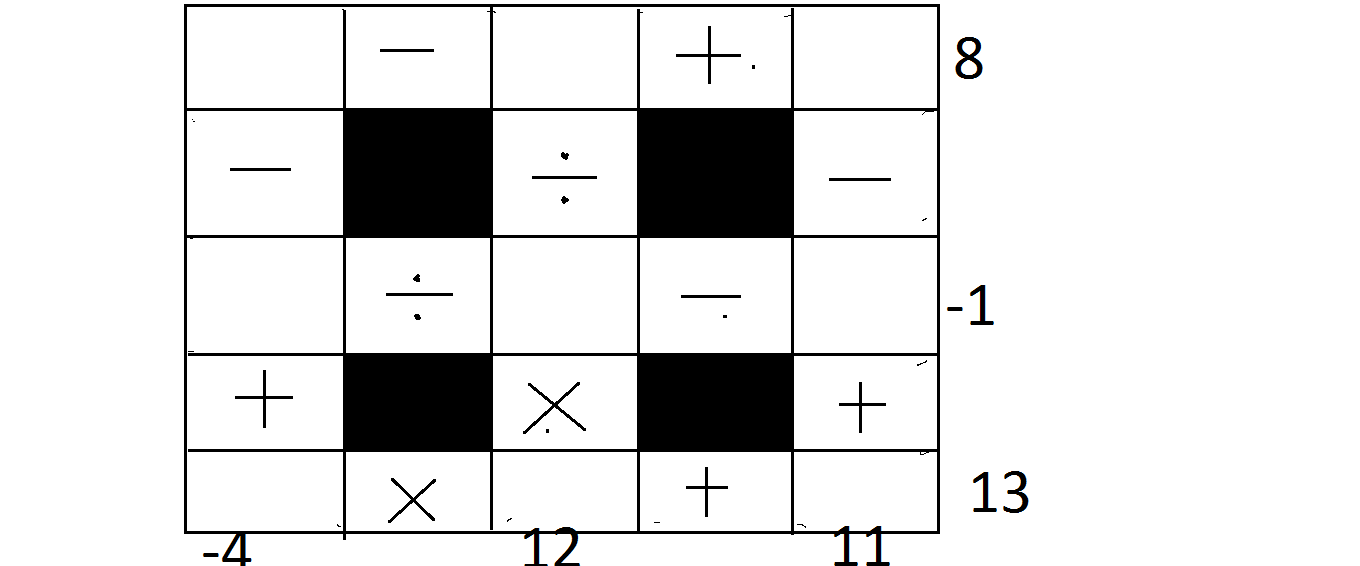
Using the digits 1 to 9 exactly once, fill in the above image such that each row and column is correct.
What is the sum of the 5 numbers in the middle row and column?
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Name the cell on x -th row and y -th column as R x C y .
From column 1, R 2 C 1 = 4 + R 1 C 1 + R 3 C 1 ≥ 4 + 1 + 2 = 7 . From column 3, R 2 C 3 = R 1 C 3 + R 3 C 3 − 1 1 ≤ 8 + 9 − 1 1 = 6 . From row 2, R 2 C 3 > R 2 C 2 R 2 C 1 . If R 2 C 2 = 1 , then 6 ≥ R 2 C 3 > R 2 C 1 ≥ 7 , contradiction. Thus R 2 C 2 ≥ 2 . Together with the fact that R 2 C 2 divides R 2 C 1 (so that row 2 results to an integer), there are only three possibilities for row 2: ( 8 , 2 , 5 ) , ( 8 , 4 , 3 ) , ( 9 , 3 , 4 ) .
Case 1 : ( R 2 C 1 , R 2 C 2 , R 2 C 3 ) = ( 9 , 3 , 4 )
Then R 1 C 1 + R 3 C 1 = 5 , and so { R 1 C 1 , R 1 C 3 } = { 1 , 4 } ∨ { 2 , 3 } . However, neither is possible, as they would repeat 4 or 3 used on R 2 C 3 and R 2 C 2 respectively. Thus this case is impossible.
Case 2 : ( R 2 C 1 , R 2 C 2 , R 2 C 3 ) = ( 8 , 4 , 3 )
Likewise, this gives R 1 C 1 + R 3 C 1 = 4 , which forces { R 1 C 1 , R 3 C 1 } = { 1 , 3 } (the other choice { 2 , 2 } is impossible, as it would repeat the same digit). But now this repeats the 3 on R 2 C 3 .
Case 3 : ( R 2 C 1 , R 2 C 2 , R 2 C 3 ) = ( 8 , 2 , 5 )
We have { R 1 C 1 , R 3 C 1 } = { 1 , 3 } and { R 1 C 3 , R 3 C 3 } = { 7 , 9 } . Thus by elimination, { R 1 C 2 , R 3 C 2 } = { 4 , 6 } , and so we already have the answer: R 1 C 2 + R 2 C 1 + R 2 C 2 + R 2 C 3 + R 3 C 2 = ( 4 + 6 ) + 8 + 2 + 5 = 2 5 .
However, of course we want to keep going and see if the solution is unique.
From row 3, R 3 C 3 ≥ 7 , so R 3 C 1 ⋅ R 3 C 2 ≤ 6 . But R 3 C 2 ≥ 4 , so R 3 C 1 ≤ 4 6 , forcing R 3 C 1 = 1 . This means R 1 C 1 = 3 .
Now, R 1 C 2 = R 1 C 1 + R 1 C 3 − 8 = R 1 C 3 − 5 ≤ 9 − 5 = 4 , but R 1 C 2 ≥ 4 . So equality is achieved, giving R 1 C 2 = 4 , and the rest is easy.
The unique solution is: